Lượng giác là một phần quan trọng của toán học và rất quan trọng trong nhiều lĩnh vực, chẳng hạn như vật lý, kỹ thuật và cả cuộc sống hàng ngày. Trong bài viết này, chúng ta sẽ xem xét 6 công thức lượng giác cơ bản mà tất cả học sinh đều nên biết. Điều này tạo điều kiện thuận lợi cho việc vượt qua các bài kiểm tra và cung cấp cho bạn nền tảng vững chắc để tiếp thu kiến thức sâu hơn sau này.
1. Giới thiệu về 6 công thức lượng giác cơ bản
Những công thức chính được sử dụng trong lượng giác, chủ yếu liên quan đến các hàm số lượng giác như sin, cos, tan, cot, sec và csc, được bao gồm trong công thức lượng giác cơ bản. Khi biết giá trị của một góc hoặc một phương trình hình học, những công thức này rất quan trọng để tính toán các giá trị của các hàm này.
Có thể nói rằng sáu công thức lượng giác cơ bản là nền tảng cho bất kỳ ai muốn học hình học hoặc bất kỳ lĩnh vực nào sử dụng toán học. Bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các vấn đề thực tế nếu bạn biết cách sử dụng chúng.
Các công thức lượng giác cơ bản
Trước tiên, hãy nêu tên sáu công thức lượng giác thông thường:
- Sin là sin(α) và cos là cos(α).
- Tan: tan(α) tương đương với sin(α)/cos(α).
- Có thể tìm thấy rằng cot(α) = 1/tan(α) = cos(α)/sin(α).
- Sec(α) = 1/cos(α).
- Trong Csc, csc(α) = 1/sin(α).
- Mỗi công thức này cung cấp thông tin quan trọng về mối quan hệ giữa các cạnh và góc của một tam giác vuông. Những tam giác này rất phổ biến trong các bài toán thực tế.
Công thức lượng giác là gì?
- Hiểu được sáu công thức lượng giác cơ bản sẽ giúp bạn giải quyết các bài toán lượng giác và cung cấp cho bạn nền tảng để tiếp cận các lĩnh vực nâng cao như đại số, hình học không gian và vật lý. Ngoài ra, lượng giác được sử dụng rộng rãi trong nhiều lĩnh vực, bao gồm điện tử, xây dựng, định vị GPS và các lĩnh vực khoa học khác.

2. Ý nghĩa của các công thức lượng giác cơ bản
Khi học về 6 công thức lượng giác, cần phải ghi nhớ chúng và hiểu ý nghĩa của chúng. Mỗi công thức trong toán học đều có mục đích cụ thể và tồn tại vì lý do cụ thể.
- Hai hàm số lượng giác cơ bản nhất là sin và cos: Hai hàm số lượng giác cơ bản mà mọi người thường bắt đầu tìm hiểu là sin và cos. Chiều cao (hay đối) của một góc trong tam giác vuông được thể hiện bằng sin của góc đó so với cạnh huyền. Ngoài ra, cos mô tả chiều dài của cạnh huyền so với cạnh kề. Điều này làm cho việc hình dung các mối quan hệ giữa các cạnh của một tam giác vuông trở nên dễ dàng hơn.
- Tan và cot: Tính toán tỉ số giữa các cạnh Tan và cot cũng rất quan trọng để tính toán và so sánh các cạnh trong tam giác vuông. Tỷ số giữa đối và kề được gọi là tan, trong khi cot là tỷ số ngược lại. Hiểu các khái niệm này sẽ cho bạn một cái nhìn tổng quát về cách các cạnh trong tam giác xa gần nhau.
- Sec và csc: Những hàm bổ sung này ít phổ biến hơn nhưng cũng rất quan trọng trong một số trường hợp. Chúng là nghịch đảo của sin và cos. Khi làm việc với các bài toán phức tạp hơn, việc sử dụng sec và csc sẽ giúp quá trình tính toán trở nên dễ dàng hơn và đơn giản hơn.
3. Hướng dẫn ghi nhớ 6 công thức lượng giác
Việc ghi nhớ chúng một cách dễ dàng là rất quan trọng để có thể sử dụng sáu công thức lượng giác cơ bản một cách hiệu quả. Đây là một số lời khuyên có thể giúp bạn ghi nhớ tốt hơn.
- Sử dụng hình ảnh để thu thập thông tin: Một hình ảnh là một trong những cách hiệu quả nhất để ghi nhớ các công thức lượng giác. Một tam giác vuông có các cạnh thể hiện sin, cos và tan có thể được vẽ. Nhớ giá trị của từng hàm số sẽ dễ dàng hơn khi bạn hình dung chúng trong một tam giác.
- Tạo một tác phẩm thơ hoặc câu chuyện: Một số học sinh thích viết thơ hoặc câu chuyện để ghi nhớ. Ví dụ, bạn có thể viết một câu chuyện ngắn về các nhân vật mà từng hàm số đại diện cho. Việc học trở nên thú vị hơn và ghi nhớ được cải thiện.
- Thực hành hàng ngày: Không có phương pháp nào tốt hơn để ghi nhớ các công thức lượng giác hơn là thực hành chúng. Mỗi ngày, hãy cố gắng giải quyết các bài toán liên quan đến lượng giác. Bạn không chỉ có thể ghi nhớ công thức tốt hơn mà còn có thể củng cố kiến thức của bạn.
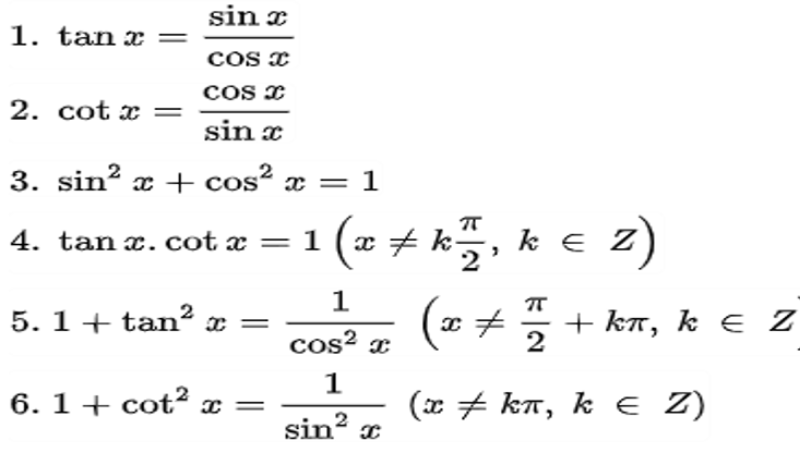
4. Ứng dụng thực tiễn của 6 công thức lượng giác cơ bản
Sau khi nắm bắt và hiểu về 6 công thức lượng giác cơ bản, bước tiếp theo là xác định các ứng dụng thực tế của chúng.
- Trong lĩnh vực kiến trúc và xây dựng: Các công thức lượng giác rất cần thiết để tính toán chiều cao, góc nghiêng và khoảng cách giữa các điểm trong kiến trúc và xây dựng. Để đảm bảo độ chính xác trong thiết kế và xây dựng một công trình, các kỹ sư thường sử dụng những công thức này.
- Về mặt vật lý: Các hiện tượng vật lý như sóng, ánh sáng và chuyển động cũng sử dụng lượng giác. Các nhà khoa học thường sử dụng hàm lượng giác để mô tả chuyển động của các hạt và dao động sóng.
- Khi nói đến lập trình máy tính: Lập trình máy tính, đặc biệt là đồ họa và game, yêu cầu lượng giác. Công thức lượng giác được các lập trình viên sử dụng để xác định vị trí và chiều hướng của các đối tượng trong không gian ba chiều.
- Đối với âm nhạc và âm thanh: Cuối cùng, lượng giác còn được sử dụng trong âm nhạc. Nguyên lý lượng giác là nền tảng cho nhiều lý thuyết về âm nhạc để phân tích và tạo ra âm thanh. Các nhạc sĩ cũng sử dụng công thức này để tạo ra hợp âm và giai điệu.
5. Bài tập thực hành với 6 công thức lượng giác
Việc thực hành giải các bài tập liên quan đến 6 công thức lượng giác cơ bản là rất quan trọng để củng cố kiến thức đã học. Bạn có thể thử một số bài tập đơn giản sau đây.
Bài đầu tiên: Tính toán các giá trị sin và cos
- Tính giá trị của sin(α + β) và cos(α + β) cho các góc α = 30 độ và α = 45 độ.
Bài tập hai: Thực hiện công thức nhân đôi
- Hãy sử dụng công thức nhân đôi để tính giá trị của sin và cos cho góc 60 độ.
Bài tập 3: Bài toán trong thế giới thực
- Một cây thẳng đứng cao mười mét. Tính góc nhìn (góc giữa mặt đất và đường thẳng nhìn từ mắt đến đỉnh cây) từ một điểm cách chân cây năm mét.
Bạn có thể củng cố kiến thức của mình và hiểu sâu hơn về ứng dụng của các công thức lượng giác bằng cách thực hiện những bài tập này.
6. So sánh 6 công thức lượng giác cơ bản
Bạn có thể hiểu rõ hơn về mối quan hệ giữa các công thức lượng giác cơ bản bằng cách so sánh chúng. Bạn sẽ có cái nhìn tổng quát hơn về lượng giác bằng cách nhận ra những điểm tương đồng và khác biệt.
- Mối quan hệ giữa sin và cos: Cos và sin rất quan trọng với nhau. Sin của một góc là cos của góc bổ sung là một đặc điểm nổi bật. Điều này có nghĩa là bạn có thể dễ dàng xác định giá trị của cos nếu bạn biết giá trị của sin và ngược lại.
- Có một sự khác biệt giữa cot và tan: Cot và tan có mối quan hệ ngược chiều với nhau. Tan là tỷ số giữa sin và cos; cot là tỷ số ngược lại. Chính vì sự khác biệt này mà chúng trở thành những công cụ rất hữu ích để giải quyết các bài toán phức tạp.
- Các hàm số thêm csc và sec: Bằng sin và cos, sec và csc không phổ biến, nhưng chúng vẫn đóng một vai trò quan trọng trong một số trường hợp. Khi bạn cần tính toán nghịch đảo của các hàm số lượng giác khác, chúng thường được sử dụng.
7. Làm thế nào để nhớ các công thức lượng giác
Nhiều học sinh có thể gặp khó khăn khi nhớ 6 công thức lượng giác cơ bản. Nhưng bạn có thể cải thiện khả năng ghi nhớ của mình.
- Ghi chú và ôn tập liên tục: Bạn sẽ nhớ lâu hơn nếu ghi lại các công thức vào một cuốn sổ tay và ôn tập chúng thường xuyên. Điều này không chỉ tăng cường khả năng ghi nhớ của bạn mà còn nâng cao khả năng suy nghĩ logic của bạn.
- Một bảng danh sách được tạo: Tạo một bảng danh sách các công thức lượng giác cùng với một ví dụ là một cách khác để ghi nhớ. Bạn có thể dễ dàng tiếp cận và học hỏi bằng cách treo bảng này ở nơi bạn thường xuyên nhìn thấy.
- Hợp tác với nhóm học tập: Bạn có thể trao đổi kiến thức và hỗ trợ lẫn nhau trong việc ghi nhớ hơn nếu tham gia vào một nhóm học tập. Bạn có thể thảo luận về các công thức lượng giác hoặc giải quyết các bài tập cùng nhau.
8. Tóm tắt 6 công thức lượng giác cơ bản
Như đã nêu, 6 công thức lượng giác cơ bản rất quan trọng để giải quyết các bài toán trong hình học, vật lý và nhiều lĩnh vực khoa học khác. Để tóm tắt, các công thức được cung cấp dưới đây:
- Sin là sin(α).
- Cơ sở cos: cos(α)
- Tan: tan(α) tương đương với sin(α)/cos(α).
- Cot(α) bằng cos(α)/sin(α).
- Sec(α) = 1/cos(α).
- Trong Csc, csc(α) = 1/sin(α).
Nắm vững các công thức này sẽ giúp bạn ứng dụng chúng trong cuộc sống hàng ngày.
9. Kết luận
Trong bài viết này, chúng tôi đã nói chi tiết về sáu công thức lượng giác cơ bản mà tất cả học sinh phải biết. Những công thức này có thể được sử dụng trong nhiều lĩnh vực khác nhau ngoài toán học. Tôi hy vọng rằng những thông tin và cách ghi nhớ mà tôi cung cấp sẽ giúp bạn tự tin hơn khi sử dụng các công thức này. Trên đây là bài viết về tìm hiểu 6 công thức lượng giác cơ bản, chi tiết xin truy cập website: congthuccapsocong.com xin cảm ơn!
