Trong toán học, công thức cấp số cộng công sai là một trong những khái niệm quan trọng nhất. Để giải quyết nhiều vấn đề khác nhau, bạn phải hiểu và áp dụng công thức chính xác này . Chúng ta sẽ cùng xem các sai sót cấp công thức và các lỗi thường gặp khi sử dụng nó trong bài viết này .
1. Công thức cấp số cộng công sai: Khái niệm và ý nghĩa
Làm thế nào để tìm ra công thức cấp số cộng sai ? Để trả lời câu hỏi này, trước tiên chúng ta phải hiểu cấp độ cộng là gì. Sai , một số giữa hai số liên tiếp , được gọi là cộng số cấp. Có thể hiểu sai công thức cộng số cấp độ là tính toán các giá trị của một số trong chuỗi với công sai không đồng nhất.
Tại sao lại cần biết công thức này?
- Biết công thức cấp số cộng công sai giúp học sinh nắm vững các khái niệm cơ bản của toán học. Họ có thể áp dụng kiến thức đã học vào các bài toán nâng cao hơn trong tương lai nhờ điều này.
- Ngoài ra, việc sử dụng công thức này đúng cách có thể giúp dự báo và phân tích trở nên chính xác hơn trong các lĩnh vực như khoa học, kinh tế hoặc kỹ thuật.
Cách áp dụng công thức trong thực tế
- Khi sử dụng công thức cấp số cộng công sai trong các trường hợp thực tế, chúng ta thường phải xem xét các yếu tố ngoại cảnh có thể ảnh hưởng đến kết quả. Tính chính xác của mọi tính toán tăng lên khi bạn biết công thức.
- Tóm lại, việc hiểu công thức cấp số cộng công sai có nhiều lợi ích lý thuyết và thực tế.
2. Cách xác định công sai trong cấp số cộng
Để tìm công sai cấp số cộng, chúng ta phải hiểu các phương pháp tính toán và sử dụng tất cả các phương pháp. Công sai là hiệu số giữa hai số liên tiếp trong dãy số. Các bước xác định sẽ phức tạp hơn khi công sai không đồng nhất.
Phương pháp tính công sai
- Đầu tiên, bạn có thể tìm thấy công sai bằng cách lấy hiệu số giữa hai số liền kề. Nếu các số đầu tiên là a_1 và số thứ hai là a_2, công sai (d) sẽ được tính như sau:
- [d = a_2, a_1]
- Tính toán công sai giữa các cặp số để xác định mối liên hệ giữa chúng khi có công sai không đồng nhất.
Ví dụ minh họa
- Giả sử dãy số có số 2, 5, 9, 14, 20.
- Để phân biệt sự khác biệt giữa hai số đầu tiên:
- Cơ sở d_1 là 5 – 2 = 3.
- Các số sau đây được tìm thấy: d_2 = 9 – 5 = 4; d_3 = 14 – 9 = 5; và d_4 = 20 – 14 = 6.
- Do đó, chúng ta thấy rằng trong trường hợp này, công sai không đồng nhất. Mỗi khi một số người được tăng lên, công sai sẽ tăng lên.
Rút ra kết luận về công sai
- Việc tìm ra công sai trong cấp số cộng không chỉ là một phép toán mà còn yêu cầu một cái nhìn toàn diện về các mối quan hệ trong dãy số. Điều này cho phép bạn đưa ra các phân tích và dự báo chính xác hơn cho nhiều bài toán.

3. Ví dụ minh họa về công thức cấp số cộng công sai
Xem xét một số ví dụ cụ thể để hiểu rõ hơn về công thức cấp số cộng công sai. Những ví dụ này không chỉ giúp bạn hình dung mà còn giúp bạn áp dụng.
Ví dụ 1: Dãy số đơn giản
Xem dãy số 1, 3, 6, 10 và 15. Có thể dễ dàng thấy rằng công sai của mỗi cặp số không giống nhau.
- Dùng cách tính công sai đã đề cập, chúng ta có:
- ( d_1 = 3 – 1 = 2 )
- ( d_2 = 6 – 3 = 3 )
- ( d_3 = 10 – 6 = 4 )
- ( d_4 = 15 – 10 = 5 )
Điều này cho thấy công sai không đều và đang tăng dần.
Ví dụ 2: Dãy số có quy luật phức tạp hơn
Tìm hiểu dãy số phức tạp hơn bao gồm 1, 4, 9, 16, 25.
Tính công sai giữa các cặp:
- Tính công sai từng cặp:
- ( d_1 = 4 – 1 = 3 )
- ( d_2 = 9 – 4 = 5 )
- ( d_3 = 16 – 9 = 7 )
- ( d_4 = 25 – 16 = 9 )
Trong dãy số này, rõ ràng là công sai không đồng nhất và tăng lên hai đơn vị mỗi bước.
Ý nghĩa của các ví dụ
- Các ví dụ trên không chỉ giúp bạn hiểu rõ hơn về cách xác định công sai mà còn giúp bạn hiểu cách áp dụng công thức trong thế giới thực. Để củng cố kiến thức của mình, hãy thử áp dụng các phương pháp này vào các dãy số khác.
4. Ứng dụng của công thức cấp số cộng công sai trong toán học
Công thức cấp số cộng công sai có nhiều ứng dụng thực tế trong toán học và các lĩnh vực khác. Những ứng dụng này làm cho chúng ta hiểu rõ hơn về các mối quan hệ giữa các số liệu và sự biến động.
- Phân tích dữ liệu: Công thức cấp số cộng công sai là một trong những công thức được sử dụng phổ biến nhất trong phân tích dữ liệu. Công thức này thường được các nhà thống kê và phân tích dữ liệu sử dụng để tìm mô hình và xu hướng trong dữ liệu. Điều này rất quan trọng khi đưa ra quyết định dựa trên số liệu.
- Giải quyết bài toán tối ưu hóa: Công thức cấp số cộng công sai giúp các nhà nghiên cứu tìm ra các biến số quan trọng trong các bài toán tối ưu hóa. Nó cũng giúp họ xác định các mối quan hệ giữa các biến số. Họ có thể cải thiện hiệu suất bằng cách phân tích công sai.
- Tạo ra mô hình dự báo: Khi xây dựng các mô hình dự báo, rất quan trọng là phải hiểu rõ công thức cấp số cộng công sai. Nó thường được sử dụng bởi các nhà phân tích để tạo ra các dự báo đáng tin cậy dựa trên dữ liệu lịch sử. Điều này đặc biệt quan trọng trong quản trị rủi ro, kinh tế và tài chính.
- Phát triển các lý thuyết toán học mới: Cuối cùng, nhiều lý thuyết toán học mới đã được tạo ra bởi công thức cấp số cộng công sai. Các nhà toán học đã phát hiện ra nhiều quy luật và tính chất mới trong các lĩnh vực khác nhau, chẳng hạn như đại số, hình học và xác suất, nhờ nghiên cứu công sai và dãy số.
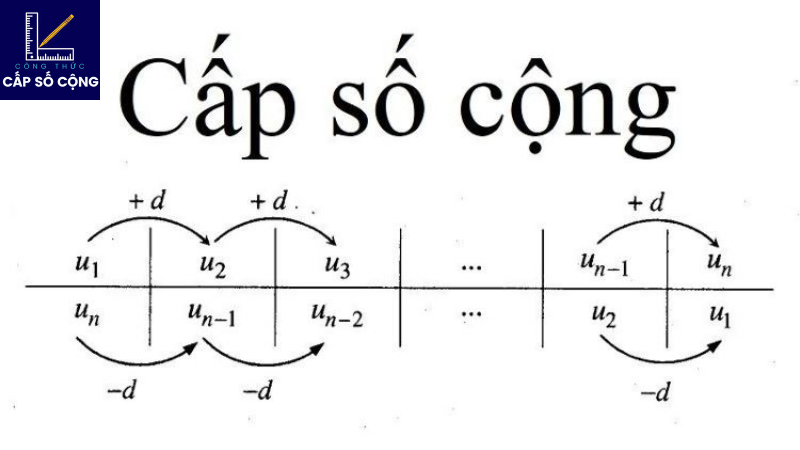
5. So sánh giữa cấp số cộng công đúng và công sai
Công thức cấp số cộng công sai phải được so sánh với công thức cấp số cộng công đúng để hiểu rõ hơn. Sự so sánh này giúp chúng ta hiểu được sự khác biệt và ứng dụng của từng loại công thức trong thế giới thực.
- Khái niệm cấp số cộng công đúng: Cấp số cộng công đúng là một dãy số có công sai hằng số giữa các số liên tiếp. Hiệu số sẽ luôn giống nhau nếu bạn lấy hai số trong dãy. Dãy số 2, 4, 6, 8, 10 là một ví dụ thông thường, trong đó công sai luôn là 2.
- Đặc điểm của cấp số cộng công sai: Công sai thay đổi giữa các số trong dãy nhờ cấp số cộng công sai lại. Điều này làm cho dãy số đa dạng và phong phú hơn. Chẳng hạn, dãy số 1, 3, 6, 10, 15 có công sai không đồng nhất và tăng lên.
- Lợi ích của việc hiểu rõ cả hai khái niệm: Nếu bạn biết cách phân biệt cấp số cộng công đúng và sai, bạn sẽ có thể áp dụng công thức đúng trong mọi tình huống. Điều này có lợi không chỉ trong giáo dục mà còn trong nghiên cứu và ứng dụng thực tiễn.
6. Lỗi thường gặp khi sử dụng công thức cấp số cộng công sai
Mặc dù công thức cấp số cộng công sai là một phương pháp hữu ích, nhưng nhiều người vẫn mắc phải một số lỗi thường xảy ra khi sử dụng nó. Những sai sót này có thể dẫn đến kết quả sai và làm giảm khả năng hiểu vấn đề.
- Tính toán sai công sai: Tính toán sai công sai là một trong những lỗi phổ biến nhất. Nhiều người không nhận ra rằng công sai có thể khác nhau giữa các số trong dãy. Do đó, họ thường không chú ý đến việc tính toán chính xác từng cặp số. Kết quả có thể sai lệch nếu rút ngắn quá trình tính toán.
- Không kiểm tra lại dữ liệu: Sau khi tính toán, nhiều người thường bỏ qua bước kiểm tra lại dữ liệu. Việc này là vô cùng quan trọng để đảm bảo rằng các kết quả được thu thập là chính xác. Kiểm tra không chỉ giúp tìm ra những sai sót mà còn giúp nâng cao kiến thức và kỹ năng.
- Nhầm lẫn công thức: Một lỗi khác phổ biến là nhầm lẫn giữa công thức cấp số cộng công đúng và sai. Nhiều người áp dụng sai công thức vì họ không biết sự khác biệt giữa hai khái niệm này. Điều này có thể dẫn đến nhầm lẫn nghiêm trọng và ảnh hưởng đến kết quả.

7. Cách khắc phục công sai trong cấp số cộng
Chúng ta cần áp dụng các phương pháp và kỹ thuật phù hợp để giải quyết các lỗi thường xảy ra khi sử dụng công thức cấp số cộng công sai.
- Kiểm tra và đánh giá lại kết quả: Sau khi thực hiện các phép tính, hãy dành thời gian để kiểm tra và đánh giá lại kết quả. Điều này không chỉ giúp tìm ra sai sót mà còn giúp bạn hiểu công thức làm thế nào. Tham khảo ý kiến của bạn bè hoặc giáo viên hoặc so sánh kết quả của bạn với các nguồn tài liệu khác.
- Thực hành thường xuyên: Khắc phục lỗi là thực hành thường xuyên. Tìm kiếm các trường hợp và công việc thực tế mà bạn có thể áp dụng công thức cấp số cộng công sai. Khi bạn thực hiện hành động, bạn sẽ quen với cách sử dụng và bạn sẽ trở nên tự tin hơn khi giải quyết các bài toán phức tạp.
- Học nhóm và thảo luận: Một cách khác để giải quyết vấn đề là tham gia vào các buổi học nhóm hoặc nói chuyện với bạn bè. Việc chia sẻ ý tưởng và kinh nghiệm sẽ giúp bạn nâng cao kỹ năng của mình và tìm ra những sai lầm của mình.
8. Kết luận
Công thức cấp số cộng sai rất hữu ích trong toán học và có nhiều ứng dụng thực tế . Bạn biết rõ về các khái niệm, ví dụ minh họa, ứng dụng , so sánh và lỗi thường gặp khi sử dụng đã được cải thiện trong bài viết này. Bài viết này sẽ giúp bạn hiểu rõ hơn về sai công thức cấp số cộng và có thể áp dụng nó trong học tập và cuộc sống .
Công thức cấp số cộng (C.S.C.) với công sai d là một trong những công cụ toán học quan trọng giúp giải quyết các bài toán liên quan đến dãy số có sự thay đổi đều đặn. Nhờ vào sự rõ ràng và đơn giản của công thức này, chúng ta có thể dễ dàng tính toán được các giá trị của các phần tử trong dãy số.
Tuy nhiên, giống như việc tính toán một cấp số cộng, sự phát triển và điều trị bệnh hen suyễn cũng đòi hỏi sự điều chỉnh cẩn thận, theo dõi thường xuyên và kiên nhẫn, chi tiết xin truy cập website: congthuccapsocong.com xin cảm ơn!
