Trong toán học, các công thức cấp số cộng là một chủ đề quan trọng và hấp dẫn. Chúng rất quan trọng để hiểu và giải quyết nhiều vấn đề thực tế, chẳng hạn như tính lãi ngân hàng và mô hình tăng trưởng dân số. Bài viết này sẽ đề cập một cách chi tiết đến các công thức cấp số cộng, bao gồm công thức tổng quát và ba ứng dụng chính của chúng trong toán học.
1. Giới thiệu về các công thức cấp số cộng
Các công thức cấp số cộng, còn được gọi là dãy số cộng, là một dãy số trong đó công sai là một số hằng định cộng với số hạng trước của nó. Các đặc trưng của các cấp số cộng, chẳng hạn như số hạng thứ n, tổng n số hạng đầu tiên, v.v., có thể được tính bằng các công thức toán học được gọi là các công thức cấp số cộng.
Định nghĩa cấp số cộng
- Một dãy số thỏa mãn điều kiện sau đây được gọi là cấp số cộng:
- a2=a1 + d a3 = a2 + d an = an−1 + d
- Nó bao gồm:
- Các số hạng của cấp số cộng d là công sai hoặc một số hằng định, như a1, a2, a3 và an.
- Do đó, số hạng tiếp theo bằng số hạng trước cộng với công sai d.
- Chẳng hạn, cấp số cộng
Ví dụ về cấp số cộng
- Các số 2, 5, 8, 11, 14 và Trong ví dụ này, a1 = 2, d = 3, và cộng thêm 3 vào số hạng trước đó để tạo ra các số hạng sau.
- Ví dụ thêm:
- -1, 1, 3, 5,… Trong ví dụ này, a1 = -3, d = 2, và cộng thêm 2 vào số hạng trước đó để tạo ra các số hạng sau.
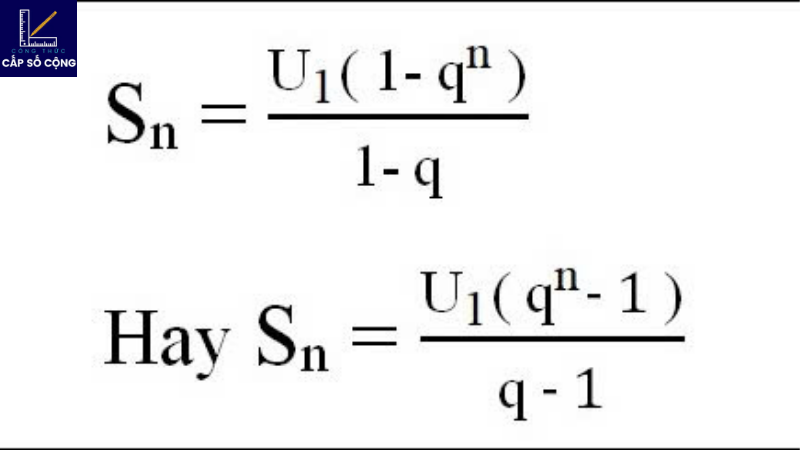
2. Công thức tổng quát của cấp số cộng
Trong việc tính toán các đặc trưng của dãy số, các công thức cấp số cộng của cấp số cộng rất hữu ích. Tìm số hạng thứ n, tổng n số hạng đầu tiên, v.v. có thể được thực hiện bằng cách sử dụng công thức này.
Công thức số hạng thứ n
Sau đây là công thức để tìm số hạng thứ n của cấp số cộng:
- an = a1 + d(n-1)
Nó bao gồm:
- Số hạng thứ n của cấp số cộng an, số hạng đầu tiên của cấp số cộng a1, công sai của cấp số cộng d và chỉ số của số hạng cần tìm n.
- Ví dụ, trong trường hợp chúng ta có cấp số cộng 2, 5, 8, 11, 14,… thì:
- a1 = 2 (số hạng đầu)
- Công sai d = 3
- Tôi muốn tìm số hạng thứ mười, và tôi có n = 10. Vì vậy, trong công thức, chúng ta có: an = a1 + (n-1)d a10 = 2 + (10-1)= 29
- Vì vậy, hạng thứ 10 trong cấp số cộng này là 29.
Công thức tổng n số hạng đầu tiên
Sau đây là công thức để tìm tổng số hạng đầu tiên của cấp số cộng:
- Sn = n/2 * (a1 + an) = n
- Nó bao gồm:
- Sn là tổng của n số hạng thứ nhất.
- Số hạng đầu tiên (a1) và số hạng thứ n
- n là số lượng các hạng cần tính tổng. Ví dụ, nếu chúng ta có cấp số cộng là 2, 5, 8, 11, 14,… và chúng ta muốn tính tổng 5 hạng đầu tiên, thì chúng ta sẽ có:
- a1= 2
- Các công thức cấp số cộng số hạng thứ n cho thấy a5 = 2 + (5-1)3 = 14 và n = 5.
- Sau đó, theo công thức, chúng ta có: Sn = n/2 (a1 + an) S5 = 5/2 (2 + 14) = 40
- Vì vậy, tổng cộng của năm số hạng đầu tiên trong cấp số cộng này là 40.
3. Các ví dụ minh họa cho công thức cấp số cộng
Chúng ta sẽ xem xét một số ví dụ cụ thể để hiểu rõ hơn về các công thức cấp số cộng
Ví dụ 1: Tính số hạng thứ n của cấp số cộng
- Giả sử chúng ta có các cấp số cộng như 3, 7, 11, 15,… Tìm số hạng thứ tám trong cấp số cộng này.
- Ta sử dụng công thức số hạng thứ n để giải quyết bài toán này: an = a1 + (n-1)d.
- Trong ví dụ sau đây:
- a1 = 3 (số hạng đầu)
- Công sai d = 4
- n = 8 (số hạng phải được tìm)
- Vì vậy, trong công thức có: a8 = a1 + (n-1)d, và a8 = 3 + (8-1).= 31
- Nói cách khác, số hạng thứ 8 của cấp số cộng là 31.
Ví dụ 2: Tính tổng n số hạng đầu tiên của cấp số cộng
Giả sử chúng ta có các cấp số cộng như sau: -2, 1, 4, 7, 10,… Hãy tính tổng số sáu hạng đầu tiên của Các công thức cấp số cộng
- Công thức tổng n số hạng đầu tiên được sử dụng để giải quyết bài toán này: Sn = n/2 * (a1 + an) = n
- Trong ví dụ sau đây:
- Số hạng đầu tiên a1 = -2.
- Tính theo công thức số hạng thứ n, an = a6 = -2 + (6-1)3 = 13 và n = 6 là số lượng số hạng cần tính tổng.
- Vì vậy, trong công thức có: Sn = n/2(a1 + an) S6 bằng 6/2 (-2 + 13) = 33
- Vì vậy, tổng cộng của sáu số hạng đầu tiên trong cấp số cộng này là 33.

4. Ứng dụng của cấp số cộng trong toán học
Trong toán học và nhiều lĩnh vực khác, các công thức cấp số cộng và các công thức liên quan đến chúng rất quan trọng. Ba ứng dụng chính sau đây:
Ứng dụng 1: Tính lãi ngân hàng
Tính toán lãi suất ngân hàng là một ví dụ thực tế về các công thức cấp số cộng Tiền gửi được gửi vào ngân hàng sẽ tăng theo cấp số cộng, với lãi suất tăng theo thời gian.
- Giả sử bạn gửi một triệu đồng vào ngân hàng với lãi suất 5% mỗi năm. Số tiền gửi sẽ đạt 2.000.000 VND sau bao nhiêu năm?
- Ta sử dụng công thức số hạng thứ n để giải quyết bài toán này: an = a1 + (n-1)d.
- Trong ví dụ sau đây:
- a1 = 1 triệu đồng (tiền gửi ban đầu)
- d là một triệu * 0,05 = 50.000 VND (lãi suất hàng năm, công sai)
- an = 2.000.000 VND (số tiền dự định)
- Theo công thức, 2.000.000 bằng 1.000.000 + (n-1).50.000 n = 21 tuổi
- Sau 21 năm, tổng số tiền gửi sẽ là 2.000.000 VND.
Ứng dụng 2: Mô hình tăng trưởng dân số
Các công thức cấp số cộng mô hình hóa sự tăng trưởng dân số, các công thức cấp số cộng cũng được sử dụng. Giả sử dân số của một quốc gia tăng với tốc độ ổn định, một cấp số cộng có thể được sử dụng để mô tả sự gia tăng này.
- Ví dụ, nếu dân số của một quốc gia là 100.000 người và tăng 2.000 người hàng năm, thì sự tăng trưởng này có thể được mô hình hóa bằng cấp số cộng:
- a1=100.000 (tổng dân số ban đầu)
- 2.000 là số người tăng lên hàng năm.
- Các công thức cấp số cộng cách sử dụng công thức số hạng thứ n, chúng ta có thể tính toán dân số của đất nước trong những năm tiếp theo.
Ứng dụng 3: Tính toán trong vật lý
Trong các tính toán vật lý, chẳng hạn như
- Tính quãng đường của một vật thể trong khi nó di chuyển với vận tốc không đổi
- xác định lượng phóng xạ còn lại trong một khoảng thời gian nhất định
- Mô hình hóa cách các vật liệu suy giảm theo thời gian
- Các công thức cấp số cộng những trường hợp này, các giá trị cần thiết có thể được tính toán bằng cách sử dụng các đặc trưng của cấp số cộng, chẳng hạn như số hạng thứ n hoặc tổng n số hạng đầu tiên.

5. Làm thế nào để xác định số hạng của cấp số cộng?
Các công thức cấp số cộng, chúng ta phải tìm ra các thông số sau:
- Hạng đầu tiên của số (a1)
- Không đúng (d)
- Số hạng đầu tiên trong dãy số là số hạng đầu tiên (a1). Công sai (d) là số hằng định được cộng vào số hạng tiếp theo.
- Chẳng hạn, trong dãy số 2, 5, 8, 11, 14…
- a1 = 2 (số hạng đầu)
- Công sai là d = 3, vì 5 = 2 + 3, 8 = 5 + 3,…
- Công thức an = a1 + (n-1)d có thể được sử dụng để tìm số hạng thứ n bất kỳ khi biết a1 và d.
Tính tổng của một cấp số cộng
Các công thức cấp số cộng để tính toán số hạng thứ n, cấp số cộng còn được sử dụng để tính toán tổng n số hạng đầu tiên. Để thực hiện điều này, ta sử dụng công thức sau:
- Sn = n/2 * (a1 + an) = n
Nó bao gồm:
- Sn là tổng của n số hạng thứ nhất.
- Số hạng đầu tiên (a1) và số hạng thứ n
- n là số lượng số hạng cần tính tổng. Ví dụ, nếu chúng ta có một cấp số cộng gồm 3, 6, 9, 12, 15,… và chúng ta muốn tính tổng tất cả các số hạng đầu tiên, chúng ta sẽ có:
- Nếu a1 = 3, a8 = 3 + (8-1)3 = 24, thì n = 8.
- Vì vậy, trong công thức, ta tìm thấy Sn = n/2 (a1 + an) S8 = 8/2 (3 + 24) = 4 * 27 = 108.
- Vì vậy, tổng số của tám hạng đầu tiên trong cấp số cộng này là 108.
Sử dụng công thức tổng để tối ưu hóa tính toán
- Một trong những lợi ích lớn nhất của việc sử dụng công thức tính tổng n số hạng đầu tiên là nó giúp giảm số lượng công việc cần thực hiện. Bạn chỉ cần xác định số hạng đầu tiên và số hạng thứ n để nhanh chóng tìm ra tổng, thay vì phải tính từng hạng một cách thủ công rồi cộng lại. Điều này không chỉ tiết kiệm thời gian mà còn làm cho các bài toán cấp số cộng trở nên chính xác hơn.
- Việc sử dụng công thức này trở nên càng quan trọng đối với các bài toán phức tạp hơn, có nhiều hạng phải được tính toán. Bạn sẽ dễ dàng hơn trong việc giải quyết các vấn đề liên quan đến cấp số cộng ở trường hoặc nơi làm việc nếu bạn học cách sử dụng công thức tính tổng.
Tổng quát hóa để hỗ trợ trong nghiên cứu
- Các công thức cấp số cộng được sử dụng trong nhiều lĩnh vực, chẳng hạn như thống kê, kinh tế và vật lý. Bạn có thể thay đổi công thức tổng cho cấp số cộng để phù hợp với nhiều loại bài toán nghiên cứu hoặc phân tích dữ liệu.
- Hiểu rõ hơn về các yếu tố ảnh hưởng đến tổng n số hạng đầu tiên sẽ giúp bạn có cái nhìn tổng quát hơn về cách các dãy số hoạt động trong thế giới thực. Chúng tăng cường phân tích và ra quyết định trong dự báo tài chính và mô hình hóa hiện tượng tự nhiên.
6. Kết luận
Các công thức cấp số cộng là một khái niệm cơ bản nhưng rất hữu ích. Vị trí quan trọng của nó trong nhiều lĩnh vực kiến thức, từ việc hiểu rõ công thức tổng quát đến việc tìm ra số hạng của cấp số cộng và tính toán tổng của n số hạng đầu tiên. Các ứng dụng thực tiễn, chẳng hạn như tính lãi suất ngân hàng, mô hình tăng trưởng dân số và các phép toán vật lý, cho thấy cấp số cộng có ảnh hưởng đáng kể đến cuộc sống hàng ngày của chúng ta.
Cuối cùng, việc hiểu và sử dụng các quy tắc của cấp số cộng có thể dẫn đến những kết quả thú vị và bất ngờ trong giáo dục và nghiên cứu. Tương tự như cách hiểu rõ cấp số cộng giúp bạn giải toán dễ dàng, việc phát hiện và điều trị sớm bệnh hắc lào cũng giúp bạn tránh được những phiền toái không đáng có,chi tiết xin truy cập website congthuccapsocong.com xin cảm ơn!

