Trong toán học, đặc biệt trong lĩnh vực đại số và số học, công thức cấp số cộng 11 là một khái niệm quan trọng và cơ bản. Một số ứng dụng trong cuộc sống dựa trên khái niệm này, ngoài việc hỗ trợ giải quyết các bài toán liên quan đến dãy số. Chúng tôi sẽ xem xét công thức cấp số cộng 11, các thành phần của nó, cách tính tổng, các ví dụ minh họa và lợi ích của việc sử dụng nó. Chúng tôi cũng sẽ so sánh nó với các công thức khác và giải quyết các bài tập thực tế.
1. Công thức cấp số cộng 11: Định nghĩa và ứng dụng
Trước tiên, chúng ta phải định nghĩa công thức cấp số cộng 11 để chúng ta có thể hiểu rõ hơn về nó.
Định nghĩa công thức cấp số cộng
- Trong cấp số cộng (CSCC), hiệu giữa hai số hạng liên tiếp luôn bằng một hằng số, được gọi là “công”. Trong trường hợp a là số hạng đầu tiên và d là công số, thì các số hạng tiếp theo có thể được tính như sau theo công thức cấp số cộng 11:
- Số hạng đầu tiên: a
- Số hạng thứ hai là a plus d.
- Số thứ ba là a + 2d
- Công số d sẽ là 11 với công thức cấp số cộng 11. Do đó, dãy số a, a + 11, a + 22,…
Ứng dụng trong cuộc sống
- Công thức cấp số cộng 11 không chỉ là lý thuyết mà còn có nhiều ứng dụng thực tế trong cuộc sống hàng ngày của chúng ta. Nó có thể được sử dụng trong quản lý tài chính, tính lãi suất cố định hoặc trong các lĩnh vực khoa học và kỹ thuật nơi các biến số phải được tính theo các quy luật nhất định.
- Các nhà quản lý tài chính thường sử dụng thông tin này để dự đoán thu nhập trong tương lai và lập kế hoạch chi tiêu hợp lý. Ngoài ra, công thức này được tìm thấy trong các bài toán liên quan đến thời gian, chẳng hạn như tính toán thời gian cần thiết để hoàn thành công việc trong một khoảng thời gian nhất định.
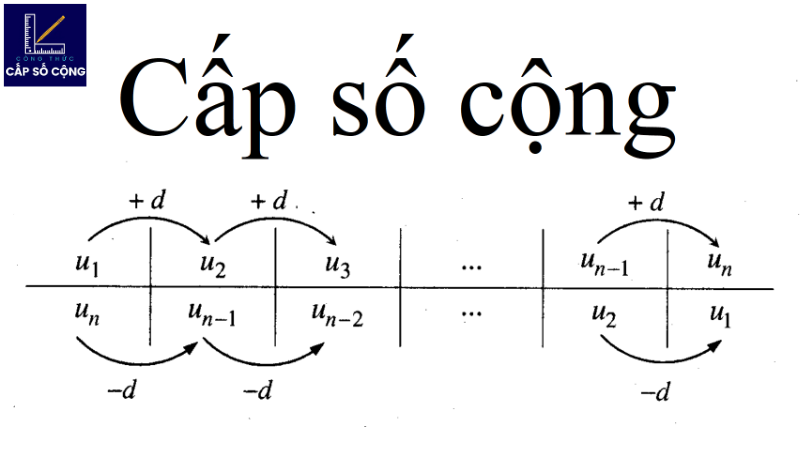
2. Các yếu tố của công thức cấp số cộng 11
Để hiểu sâu hơn về công thức cấp số cộng 11, chúng ta phải xem xét các thành phần của nó.
Số hạng đầu tiên
- Trong cấp số cộng, yếu tố quan trọng nhất là số hạng đầu tiên (hay a). Dãy số bắt đầu ở đây. Toàn bộ dãy số có thể bị ảnh hưởng đáng kể bởi giá trị của số hạng đầu tiên. Quy luật quy định rằng khi số hạng đầu tiên thay đổi, các số hạng tiếp theo cũng sẽ thay đổi theo cách tương tự.
- Khi sử dụng công thức cấp số cộng 11, việc chọn số hạng đầu tiên đúng đắn sẽ ảnh hưởng đến cách bạn tạo ra dãy số và kết quả cuối cùng.
Công số
- Giá trị chênh lệch giữa hai số hạng liên tiếp trong dãy số được gọi là công số (hay d). Công số d luôn bằng 11. Điều này có nghĩa là số lượng đơn vị trong mỗi hạng sẽ tăng lên mười một đơn vị so với trước đây.
- Công số không chỉ quan trọng đối với việc tạo ra dãy số mà còn cho phép người dùng hiểu rõ hơn về tốc độ tăng trưởng của dãy số. Một số lượng lớn sẽ dẫn đến tăng trưởng nhanh chóng, trong khi một số lượng nhỏ sẽ dẫn đến tăng trưởng chậm hơn.
Số hạng cuối cùng
- Ngoài ra, hạng cuối cùng (n) của dãy số cấp số cộng 11 có ý nghĩa quan trọng. Bạn cần biết số hạng trong dãy để tính tổng hay bất kỳ giá trị nào khác. Chiều dài của dãy số sẽ được xác định bởi số hạng cuối cùng. Sau đó, nó sẽ ảnh hưởng đến tổng và các giá trị trung bình.
- Bạn sẽ dễ dàng áp dụng công thức cấp số cộng 11 nếu bạn hiểu ba điều này.
3. Cách tính tổng trong cấp số cộng 11
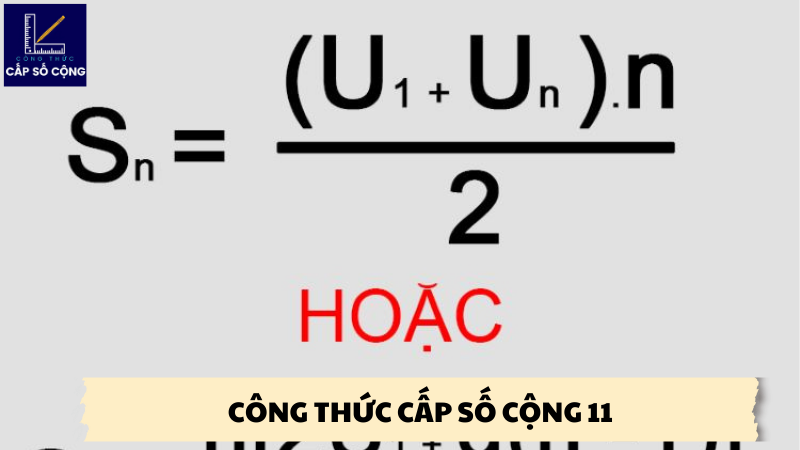
Khả năng tính tổng số hạng trong dãy số của công thức cấp số cộng 11 là một trong những sử dụng quan trọng nhất của nó. Công thức sau đây có thể được sử dụng để tính tổng của một cấp số cộng: Tổng được tính bằng (số hạng đầu + số hạng cuối).) * Tổng số số hạng / 2
Giải thích công thức tính tổng
- Nguyên lý tổng hợp các số hạng là cơ sở cho công thức trên. Chúng ta có thể tìm ra giá trị trung bình của hai số này bằng cách cộng số hạng đầu tiên và cuối cùng. Sau đó, bạn có thể lấy tổng tất cả các số hạng bằng cách nhân với số lượng các hạng và chia đôi chúng.
- Điều này cho thấy rằng công thức cấp số cộng 11 không chỉ là một phương pháp tính toán mà còn là một phương pháp hợp lý và khoa học.
Ví dụ cụ thể
- Giả sử số hạng đầu tiên là 5, chúng ta muốn tính tổng của 10 hạng đầu tiên trong dãy số cấp số cộng 11.
- Hạng đầu tiên là năm.
- Số hạng cuối cùng là 5 plus 11.:*(10-1)=5 + 99=104
- Có mười hạng.
- Đối với công thức:
- Tổng cộng là (5 + 104) * 10/2*1090
- Do đó, tổng của 10 số đầu tiên trong dãy số cấp số cộng 11 với 5 số đầu tiên sẽ là 1090.

4. Ví dụ minh họa về công thức cấp số cộng 11
Để làm rõ hơn về công thức cấp số cộng 11, chúng tôi sẽ xem xét một số ví dụ cụ thể.
Ví dụ 1: Tạo một dãy số
- Giả sử bạn muốn tạo ra một dãy số bắt đầu từ 0 và kết thúc bằng công số 11. Dãy số này sẽ như sau:
- 1, 11, 22, 33, 44, 55, 66, 77, 88, 99, 110
- Như bạn có thể thấy, tổng số hạng của dãy đã tăng lên mỗi hạng mười một đơn vị. Việc nhận diện các số hạng trở nên dễ dàng hơn do điều này.
Ví dụ 2: Tính tổng và ứng dụng
Tiếp tục với dãy số trên, chúng ta sẽ tìm ra tổng số của sáu số đầu tiên:
- 11 + 22 + 33 + 44 + 55 = 0
- Ta có thể sử dụng phương pháp tính tổng truyền thống hoặc áp dụng công thức đã được nêu ở phần trước.
- Không có hạng nhất.
- Các hạng cuối cùng là 55
- Có 6 hạng.
- Vận hành công thức sau:
- Tổng số là (0 + 55) 6*2 = 165
Ví dụ 3: Thay đổi số hạng đầu
Giả sử hạng đầu tiên của bạn là 5 và công số tiếp tục là 11. Sau đây là dãy số của bạn:
- 5–16, 27–38, 49–60, 71–82, 93–104
- Tất cả các số hạng tiếp theo sẽ thay đổi khi số hạng đầu tiên thay đổi. Mặt khác, số lượng vẫn không thay đổi, tăng thêm mười một.
5. Lợi ích của việc sử dụng công thức cấp số cộng 11
Công thức cấp số cộng 11 mang lại nhiều lợi ích đáng kể, không chỉ trong toán học mà còn trong cuộc sống hàng ngày.
Tính toán đơn giản và nhanh chóng
- Khả năng tính toán đơn giản và nhanh chóng là một trong những lợi ích lớn nhất của công thức cấp số cộng 11. Bạn có thể tính toán tổng của dãy số mà không cần phải cộng từng hạng lại với nhau bằng cách sử dụng công thức và các yếu tố liên quan.
- Thao tác này không chỉ tiết kiệm thời gian mà còn giảm nguy cơ sai sót trong quá trình tính toán.
Ứng dụng đa dạng
- Nhiều lĩnh vực, chẳng hạn như quản lý, khoa học, kỹ thuật và tài chính, sử dụng công thức cấp số cộng 11. Khả năng áp dụng công thức này trong nhiều tình huống giúp giải quyết vấn đề dễ dàng hơn.
- Chẳng hạn, các nhà nghiên cứu trong lĩnh vực tài chính có thể sử dụng công thức này để tính toán lãi suất hoặc tạo ra các dự báo kinh tế. Ngoài ra, nó có thể giúp quản lý nguồn lực hoặc lập kế hoạch sản xuất.
Phát triển tư duy logic
- Khám phá và sử dụng các công thức cấp số cộng cũng có lợi cho khả năng giải quyết vấn đề và tư duy logic. Bạn sẽ học cách đưa ra một giải pháp hợp lý bằng cách phân tích các yếu tố của một bài toán. Kỹ năng này có lợi trong học tập và cuộc sống hàng ngày.
6. So sánh công thức cấp số cộng 11 với các công thức khác
Tính toán và giải quyết dãy số có nhiều công thức toán học khác nhau. Một bản so sánh ngắn gọn giữa công thức cấp số cộng 11 và một số công thức khác được hiển thị dưới đây.
- Công thức cấp số nhân: Công thức cấp số nhân (CSMN), trái ngược với công thức cấp số cộng, là một dãy số với mỗi hạng là tích của số hạng trước đó với một hằng số. Công thức này khá phức tạp và người dùng cần có kiến thức về phép nhân. Ví dụ, dãy số 2, 4, 8, 16, 32 là một cấp số nhân với 2.
- Công thức hình học: Công thức hình học, mặc dù thường liên quan đến các yếu tố như diện tích và thể tích của các hình, cũng rất quan trọng trong toán học. Mặc dù chúng không liên quan trực tiếp đến dãy số, nhưng các thông số liên quan đến hình học có thể được tính toán bằng cách sử dụng công thức cấp số cộng.
- Công thức Fibonacci: Trong công thức Fibonacci, một dãy số có mỗi hạng là tổng của hai hạng trước đó. Dãy số này thường được tìm thấy trong nghệ thuật và thiên nhiên. Mặc dù cả hai đều nói về các quy luật số học, nhưng công thức Fibonacci cung cấp một quan điểm hoàn toàn khác.
7. Giải bài tập với công thức cấp số cộng 11
Chúng ta sẽ cùng giải một số bài tập thực tế để củng cố kiến thức về công thức cấp số cộng 11.
- Bài tập 1: Tính tổng dãy số: cho dãy số có số hạng đầu tiên là 10 và số công số là 11. tính tổng của mười lăm số đầu tiên.
- Bài tập 2: Tìm số hạng thứ n: Dãy số cấp số cộng có số hạng đầu tiên là 25 và số công số là 11. Tìm dãy số có số hạng thứ 20.
- Bài tập 3: Ứng dụng trong thực tế: Một nhà đầu tư dành 100 triệu đồng hàng tháng cho một quỹ đầu tư trong suốt mười hai tháng. Số tiền đầu tư tăng thêm 11 triệu đồng mỗi tháng. Tính toán tổng số tiền mà nhà đầu tư đã đầu tư trong suốt mười hai tháng.
Các bài tập này cho phép bạn củng cố kiến thức của mình về công thức cấp số cộng 11 và áp dụng lý thuyết vào thực tế.
8. Kết luận
Công thức cấp số cộng 11 không chỉ là một khái niệm toán học mà còn là một phương pháp mạnh mẽ để giải quyết các bài toán trong thế giới thực. Công thức này cung cấp cho người học nhiều cơ hội, từ việc tăng cường tư duy logic đến hỗ trợ tính toán nhanh chóng.
Tuy nhiên, trong một tình huống không liên quan đến toán học, như bệnh sán chó, việc hiểu về chuỗi và quy luật có thể giúp bạn nắm bắt được các mối liên hệ phát triển của bệnh và cách ngăn ngừa nó hiệu quả hơn, mặc dù đây không phải là ứng dụng trực tiếp của công thức cấp số cộng, chi tiết xin truy cập website congthuccapsocong.com xin cảm ơn!