Công thức cấp số cộng cấp số nhân là hai khái niệm cơ bản trong toán học nhưng vô cùng mạnh mẽ, và chúng có thể được tìm thấy trong nhiều lĩnh vực khác nhau, từ tài chính đến khoa học tự nhiên. Hiểu rõ hai loại công thức này không chỉ giúp giải quyết các bài toán phức tạp mà còn giúp khám phá các quy luật ẩn sau các hiện tượng xã hội và tự nhiên.
1. Công thức cấp số cộng cấp số nhân: Khái niệm và ứng dụng
Công thức cấp số cộng cấp số nhân là một khái niệm đơn giản nhưng nó có nhiều điều thú vị trong đó. Các dãy số thường có mỗi số hạng (ngoại trừ số hạng đầu tiên) được tạo ra bằng cách cộng thêm một số không đổi vào số hạng trước đó. Bản chất của cấp số cộng là do cái “số không đổi” này, còn được gọi là công sai.
Định nghĩa và các thành phần cơ bản
- Công thức cấp số cộng cấp số nhân là một dãy số có hiệu là một hằng số giữa hai số hạng liên tiếp. Hằng số này được gọi là công sai và thường được biểu thị bằng chữ d. Nếu một cấp số cộng có số hạng đầu tiên là u1, thì các số hạng tiếp theo là u2 = u1 + d, u3 = u2 + d = u1 + 2d, v.v.
- Công thức cấp số cộng cấp số nhân để tìm số hạng thứ n của cấp số cộng (un) là un = u1 + (n – 1)d. Tính chất này giúp tìm bất kỳ số hạng nào trong dãy số miễn là chúng ta biết số hạng đầu tiên và công sai.
Ứng dụng trong các bài toán thực tế
- Các vấn đề thực tế thường xuyên xảy ra mà việc áp dụng cấp số cộng mang lại lời giải đơn giản và hiệu quả.
- Chẳng hạn, số tiền lãi mà một người gửi tiết kiệm có lãi suất đơn giản sẽ không thay đổi trong mỗi kỳ thanh toán, tạo thành một cấp số cộng. Tương tự như vậy, nếu một người leo núi leo được một độ cao nhất định mỗi giờ, thì độ cao mà người đó đạt được sau mỗi giờ sẽ được cộng thành một cấp số cộng.
Công thức tổng quát và ví dụ minh họa
- Công thức cấp số cộng cấp số nhân tổng n số hạng đầu tiên của cấp số cộng, Sn = n/2 (u1 + un) hoặc Sn = n/2 [2u1 + (n-1)d), cho phép chúng ta nhanh chóng tính tổng các số hạng. Mặt khác, công thức tổng quát của cấp số cộng, un = u1 + (n Để hiểu rõ hơn, hãy xem ví dụ sau: Một người bắt đầu tiết kiệm 100.000 đồng mỗi tháng và tiết kiệm thêm 20.000 đồng mỗi tháng sau đó so với tháng trước.
- Với số hạng đầu tiên u1 bằng 100.000 và công sai d bằng 20.000, đây là một ví dụ điển hình về cấp số cộng. Số tiền tiết kiệm được trong tháng thứ mười hai sau một năm, tức là u12 = 100.000 + (12-1)20.000 = 320.000. Sau mười hai tháng, số tiền tiết kiệm được sẽ là S12 = 12/2 (100.000 + 320.000) = 2.520.000. Ví dụ này cho thấy sự hữu dụng của các công thức cấp số cộng trong việc giải quyết tăng trưởng tuyến tính và tích lũy.

2. Công thức cấp số nhân: Tính chất và ví dụ
Công thức cấp số cộng cấp số nhân, một khái niệm toán học hấp dẫn khác. Công bội là một cấp số nhân có các hạng tăng hoặc giảm theo một tỷ lệ nhất định. Ngược lại, cấp số cộng có các hạng tăng hoặc giảm theo một lượng cố định. Khái niệm này có ý nghĩa trong nhiều lĩnh vực, không chỉ trong toán học.
Định nghĩa và các thành phần cơ bản
- Trong cấp số nhân, tỉ số giữa hai hạng liên tiếp là một hằng số. Hằng số này được gọi là công bội và thường được biểu thị bằng ký hiệu q. Nếu một cấp số nhân có số hạng đầu tiên là u1, thì các số hạng tiếp theo là u2 = u1 q, u3 = u2 q = u1 q^2 và v.v.
- Công thức: un = u1 q^(n-1) thường được sử dụng để tìm số hạng thứ n của cấp số nhân (un). Phân tích và dự đoán tăng trưởng hoặc suy giảm theo cấp số nhân có thể được thực hiện bằng công thức này.
Tính chất của cấp số nhân
- Công thức cấp số cộng cấp số nhân có nhiều đặc điểm độc đáo và hữu ích trong toán học và trong thế giới thực. Một đặc điểm quan trọng là tích của hai số hạng cách đều số hạng đầu và cuối bằng bình phương số hạng giữa.
- Trong một trường hợp cụ thể, nếu số hạng thứ k cách đều hai số hạng thứ i và thứ j, thì uk^2 = ui*uj. Tính năng này có thể được sử dụng để tìm các số hạng không có trong một cấp số nhân hoặc để hiển thị các đẳng thức tương ứng.
Ví dụ minh họa về cấp số nhân
- Chúng ta hãy xem một ví dụ cụ thể để làm rõ hơn về cấp số nhân. Giả sử một quần thể vi khuẩn có số lượng vi khuẩn tăng gấp đôi mỗi giờ. Nếu ban đầu có 100 vi khuẩn (u1 = 100), thì sau 1 giờ số lượng sẽ là 200 (u2 = 100 2), sau 2 giờ sẽ là 400 (u3 = 100 2^2) và v.v. Sau n giờ, công thức tổng quát cho số lượng vi khuẩn sẽ là un = 100 * 2^(n-1), với công bội q = 2.
- Ví dụ này cho thấy sức mạnh của cấp số nhân trong việc mô tả sự tăng trưởng theo cấp số mũ, trong đó số lượng vi khuẩn tăng lên nhanh chóng theo thời gian. Ví dụ này có thể được sử dụng không chỉ trong sinh học mà còn có thể được sử dụng trong tài chính, công nghệ và nhiều lĩnh vực khác. Để hiểu được các hiện tượng tăng trưởng theo hàm mũ trong thế giới xung quanh chúng ta, cấp số nhân chính là rất quan trọng.
3. So sánh công thức cấp số cộng và cấp số nhân
Công thức cấp số cộng cấp số nhân có vẻ đơn giản, nhưng chúng có tầm quan trọng đáng kể để mô tả các yếu tố của thế giới. Mặc dù cả hai đều có quy luật, nhưng cách chúng phát triển khác nhau. Hiểu sự khác biệt này giúp chúng ta giải quyết các bài toán toán học và phân tích và dự đoán các sự kiện trong cuộc sống.
Sự khác biệt về cơ chế tăng trưởng
- Cơ chế tăng trưởng của cấp số nhân là điểm khác biệt chính giữa chúng. Trong cấp số cộng, mỗi số hạng được tạo ra bằng cách cộng thêm một hằng số (công sai) vào số hạng trước đó, điều này dẫn đến sự tăng trưởng tuyến tính.
- Điều này cho thấy rằng khoảng cách giữa các hạng liên tiếp không thay đổi, tạo thành một dãy số thay đổi đều đặn. Tuy nhiên, mỗi hạng được tạo ra bằng cách nhân với một hằng số (công bội) vào số hạng trước đó, và cấp số nhân tăng theo cấp số mũ.
Công thức tổng quát và ý nghĩa
- Sự khác biệt trong cơ chế tăng trưởng giữa các cấp số cộng và nhân cũng được thể hiện bằng công thức tổng quát của cả hai cấp số. Khi sử dụng cấp số cộng, công thức un = u1 + (n-1)d cho thấy số hạng thứ n được tạo thành bằng cách cộng nhiều lần công sai d vào số hạng đầu tiên u1.
- Tuy nhiên, công thức cấp số nhân un = u1 * q^(n-1) cho thấy rằng số hạng thứ n được tạo thành bằng cách nhân số hạng đầu tiên u1 với công bội q mũ (n-1).
So sánh về ứng dụng và hạn chế
- Cấp số cộng thường được sử dụng trong lãi suất đơn, tăng trưởng đều đặn và các thao tác số học.
- Tuy nhiên, cấp số nhân xuất hiện trong các bài toán liên quan đến lãi suất kép, phân rã phóng xạ, phát triển dân số hoặc những nơi thay đổi không diễn ra theo cách tuyến tính.

4. Cách giải bài toán với công thức cấp số cộng
Công thức cấp số cộng cấp số nhân không chỉ là việc sử dụng công thức máy móc; nó là một quá trình suy nghĩ và xem xét một vấn đề. Xác định các thông tin cần thiết cho bài toán và lựa chọn phương pháp giải phù hợp là rất quan trọng. Mỗi bước, từ việc xác định số hạng đầu, công sai và tổng của các hạng, đều đòi hỏi sự chính xác và cẩn thận.
Xác định các yếu tố của cấp số cộng từ dữ kiện bài toán
- Bước đầu tiên trong việc giải quyết một bài toán về cấp số cộng là thu thập các thành phần cơ bản của nó từ dữ kiện của bài toán. Số hạng đầu tiên (u1), công sai (d), số lượng số hạng (n) và số hạng thứ n (un) là những yếu tố này.
- Đôi khi, bài toán sẽ cung cấp thông tin gián tiếp thay vì trực tiếp cung cấp các yếu tố. Ví dụ, nó có thể cung cấp hiệu giữa hai số hạng không liên tiếp hoặc tổng của một số số hạng nhất định.
Sử dụng công thức tổng quát và công thức tính tổng
- Sau khi tìm ra các thành phần cơ bản của cấp số cộng, bước tiếp theo là giải bài toán bằng cách sử dụng các công thức tổng quát và tính tổng.
- Công thức tổng quát của cấp số cộng, un = u1 + (n – 1)d, cho phép tìm bất kỳ số hạng thứ n nào trong dãy số miễn là chúng ta biết số hạng đầu tiên và công sai của nó. Khi các bài toán yêu cầu tìm kiếm một số hạng nhất định, công thức này đặc biệt hữu ích.
Bài tập ví dụ và phân tích cách giải
- Chúng ta hãy xem xét một ví dụ sau để minh họa cách giải quyết một bài toán bằng công thức cấp số cộng: Số hạng thứ 3 của một cấp số cộng là 5 và số hạng thứ 7 là 17. Tìm số đầu tiên và công sai của cấp số cộng này.
- Chúng ta sẽ sử dụng công thức tổng quát và phân tích dữ kiện đề bài để giải bài toán này. Từ dữ kiện “số hạng thứ ba là 5”, chúng ta có thể tìm thấy rằng u3 = u1 + 2d = 5. Từ dữ kiện “số hạng thứ 7 là 17”, chúng ta có thể tìm thấy rằng u7 = u1 + 6d = 17.
5. Ứng dụng thực tiễn của công thức cấp số nhân
Công thức cấp số cộng cấp số nhân không chỉ là một khái niệm trong toán học trừu tượng mà còn là một công cụ mạnh mẽ được sử dụng đa dạng trong nhiều lĩnh vực khác nhau của cuộc sống. Khi nói đến các hiện tượng tăng trưởng hoặc suy giảm theo cấp số mũ, cấp số nhân rất quan trọng trong các lĩnh vực từ tài chính đến kinh tế, công nghệ và khoa học tự nhiên.
Lãi suất kép và tăng trưởng tài chính
- Tài chính, đặc biệt là với lãi suất kép, là một trong những lĩnh vực sử dụng phổ biến nhất của cấp số nhân. Lãi suất kép là loại lãi mà tiền lãi của một kỳ sau đó sẽ được cộng vào vốn gốc để tính lãi cho kỳ tiếp theo. Điều này tạo thành một quá trình tăng trưởng theo cấp số nhân.
- Với lãi suất kép, công thức sau đây có thể được sử dụng để tính số tiền sau n kỳ gửi là An = A0 *(1 + r)^n, trong đó A0 là số tiền gốc, r là lãi suất theo kỳ và n là số kỳ gửi.
Sự phát triển dân số và các hiện tượng sinh học
- Khoa học tự nhiên, đặc biệt là các hiện tượng sinh học và sự phát triển dân số, sử dụng cấp số nhân ngoài lĩnh vực tài chính. Thông thường, sự phát triển dân số được mô tả bằng cách sử dụng cấp số nhân, trong đó số lượng dân số tăng lên theo một tỷ lệ nhất định trong mỗi khoảng thời gian.
- Tuy nhiên, cần lưu ý rằng mô hình này thường chỉ đúng trong một thời gian nhất định vì các yếu tố khác như dịch bệnh, nguồn lực hạn chế hoặc các chính sách của chính phủ có thể ảnh hưởng đến tốc độ tăng trưởng dân số.
Ứng dụng trong công nghệ và đời sống hàng ngày
- Công thức cấp số cộng cấp số nhân được sử dụng rộng rãi trong công nghệ và đời sống hàng ngày, không chỉ trong tài chính và khoa học tự nhiên.
- Chẳng hạn, định luật Moore, quy định rằng số lượng transistor trong một chip vi xử lý sẽ tăng lên gấp đôi trong một khoảng thời gian nhất định, được sử dụng để mô tả sự phát triển của vi mạch và công nghệ máy tính. Điều này cho thấy sự phát triển nhanh chóng trong những năm gần đây của công nghệ thông tin.
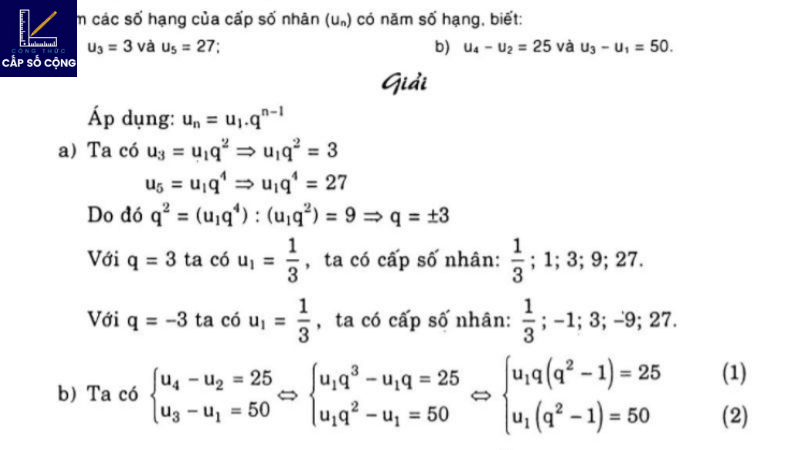
6. Hướng dẫn tìm công thức tổng quát cho cấp số cộng
Công thức cấp số cộng cấp số nhân không chỉ là một bài tập toán học mà còn giúp chúng ta hiểu rõ hơn về bản chất của dãy số này. Chúng ta sẽ tìm ra công thức chung cho cấp số cộng từ việc quan sát các hạng đầu tiên và xác định mối liên hệ giữa chúng.
Phân tích quy luật của các số hạng
- Công thức cấp số cộng cấp số nhân là bước đầu tiên trong việc tìm ra công thức tổng quát cho cấp số cộng. Điều này liên quan đến việc xem xét cách các số hạng được tạo ra từ các số hạng trước đó.
- Công thức cấp số cộng cấp số nhân, mỗi số hạng (ngoại trừ số hạng đầu tiên) được tạo ra bằng cách cộng thêm một hằng số, còn được gọi là công sai, vào số hạng trước đó.
Suy luận và xây dựng công thức
- Sau khi phân tích các quy luật của các số hạng, chúng ta sẽ tiến hành suy luận và tạo ra công thức tổng quát. Chúng tôi biết rằng u1 là số hạng thứ nhất.
- Các hạng thứ hai sẽ là u1 + d, hạng thứ ba sẽ là u1 + 2d và v.v. Quan sát cho thấy hệ số của d luôn nhỏ hơn số thứ tự của số hạng đó trong một đơn vị.
Kiểm tra và áp dụng công thức
- Sau khi tạo ra công thức cấp số cộng cấp số nhân, chúng ta phải kiểm tra tính đúng đắn của nó bằng cách áp dụng nó cho các tình huống riêng biệt.
- Chúng ta có thể sử dụng công thức để bổ sung các giá trị n khác nhau. Sau đó, chúng ta có thể so sánh kết quả với các số hạng tương ứng của cấp số cộng đã biết. Công thức của chúng tôi là chính xác nếu kết quả phù hợp với các số hạng đã biết.
7. Kết luận
Công thức cấp số cộng cấp số nhân, là những công cụ mạnh mẽ giúp chúng ta hiểu rõ hơn về thế giới xung quanh chúng ta. Hai cấp số này, từ những quy luật tăng trưởng đơn giản đến các hiện tượng phức tạp, đều đóng một vai trò quan trọng.
Cả hai công thức này không chỉ xuất hiện trong toán học thuần túy mà còn được ứng dụng rộng rãi trong tài chính, kỹ thuật và thậm chí là trong mô hình hóa sự lây lan của dịch bệnh. Giống như cách mà một bệnh dịch như bệnh phong từng lan rộng theo cấp số nhân trong lịch sử, việc hiểu rõ bản chất của các cấp số này giúp chúng ta dự đoán và kiểm soát tình huống một cách hiệu quả, chi tiết xin truy cập website congthuccapsocong.com xin cảm ơn!

