Khái niệm về cấp số cộng trong chương trình toán học lớp 11 không chỉ là một phần quan trọng trong lý thuyết mà còn rất quan trọng đối với việc giải quyết các bài toán trong thế giới thực. Cấp số cộng và công thức của nó không chỉ là những con số mà còn là những kiến thức giúp chúng ta hình dung và hiểu rõ hơn về cách toán học ảnh hưởng đến cuộc sống hàng ngày của chúng ta. Bạn sẽ học công thức cấp số cộng lớp 11 trong bài viết này, từ ý nghĩa cho đến ứng dụng thực tế, để giúp bạn nắm vững kiến thức và chuẩn bị cho kỳ thi.
1. Giới thiệu về công thức cấp số cộng lớp 11
Một dãy số có đặc điểm nổi bật là sự chênh lệch giữa các hạng liên tiếp là giống nhau được gọi là công thức cấp số cộng lớp 11. Điều này tạo ra một cấu trúc rất đặc biệt hỗ trợ tính toán. Học sinh thường được yêu cầu làm quen với khái niệm này bằng cách áp dụng nó vào các bài tập đại số hoặc giải quyết các vấn đề thực tế khi họ đang ở lớp 11.
Ý tưởng này liên quan đến nhiều vấn đề toán học phức tạp hơn chứ không chỉ là một dãy số đơn giản. Cấp số cộng cũng tạo điều kiện thuận lợi cho tư duy logic và khả năng phân tích của chúng ta. Những kỹ năng này tạo nền tảng vững chắc cho việc học toán nâng cao sau này.
Ý tưởng cơ bản về cấp số cộng
- Một dãy số có hiệu không đổi của hai số hạng liền kề được gọi là cấp số cộng, còn được gọi là dãy số cộng. Nếu a là số hạng đầu tiên và d là công sai, thì dãy số cộng như sau: a, a+d, a+2d, a+3d,…
- Trong trường hợp d dương hoặc âm, các hạng của dãy số cộng sẽ tăng lên hoặc giảm đi theo sự di chuyển của dãy số cộng. Điều này làm cho các số hạng liên kết chặt chẽ với nhau. Điều này giúp tính toán dễ dàng tổng hay bất kỳ số hạng nào.
Tính chất của cấp số cộng
- Cấp số cộng có các đặc điểm thú vị. Chẳng hạn, nếu bạn biết số hạng đầu tiên và công sai, bạn có thể tìm bất kỳ số hạng nào trong dãy mà không cần phải tính toán từng hạng một. Điều này rất hữu ích khi giải quyết các bài toán phức tạp hơn mà không mất nhiều thời gian.
- Ngoài ra, một công thức khá đơn giản được sử dụng để tìm tổng của n số hạng đầu tiên trong cấp số cộng: [S_n = frac{n}{2} cdot (a + l) ]
- Trong đó, S_n là tổng của n hạng đầu, a là hạng đầu tiên và l là hạng cuối cùng trong n hạng đầu.
Các ứng dụng của cấp số cộng
- Cấp số cộng được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau, chẳng hạn như kỹ thuật, kinh tế và khoa học. Tài chính, ví dụ, có thể sử dụng cấp số cộng để tính toán lợi nhuận hoặc khoản lãi suất theo thời gian. Ngoài ra, cấp số cộng có thể được sử dụng để mô tả các mẫu chuyển động trong vật lý.
- Học sinh được trang bị với kiến thức về cấp số cộng không chỉ giúp giải quyết các bài toán trong sách giáo khoa mà còn có thể áp dụng kiến thức này trong cuộc sống thực tế.

2. Các loại công thức cấp số cộng lớp 11
Học sinh cần nghiên cứu và làm quen với nhiều loại cấp số cộng khác nhau trong chương trình Toán lớp 11. Mỗi loại cấp số cộng có những đặc điểm và mục đích khác nhau.
Cấp số cộng vô hạn
- Dãy số có số hạng liên tiếp được tạo ra liên tục được gọi là cấp số cộng vô hạn. Do đó, khi n tiến tới vô cực, dãy số này vẫn có thể được tính toán để tìm giới hạn hoặc tổng.
- Trong các bài toán liên quan đến chuỗi số, cấp số cộng vô hạn thường xuất hiện và việc tìm kiếm tổng là một thách thức lớn. Để giải quyết loại bài toán này, học sinh phải hiểu về tính hội tụ và giới hạn.
Cấp số cộng hữu hạn
- Cấp số cộng hữu hạn chỉ bao gồm một số hạng nhất định, khác với cấp số cộng vô hạn. Tính toán tổng của dãy này thường dễ dàng hơn và đơn giản hơn.
- Bài toán liên quan đến cấp số cộng hữu hạn thường xảy ra với học sinh trong lớp mười một. Học sinh có cơ hội phát triển kỹ năng tính toán và củng cố hiểu biết về công thức tổng quát nhờ điều này.
Cấp số cộng không đều
- Cấp số cộng không đều là các dãy số mà sự khác biệt giữa các hạng vẫn có mối quan hệ, nhưng sự khác biệt giữa các hạng không đồng nhất. Điều này khiến việc xây dựng công thức và tính toán trở nên khó khăn hơn.
- Học sinh thường được yêu cầu sử dụng tư duy sáng tạo và khả năng phân tích để xác định và xử lý loại cấp số cộng này. Mặc dù loại dãy số này không phổ biến trong các bài tập, nhưng biết cách sử dụng loại số này sẽ rất hữu ích trong thực tế.
3. Ví dụ minh họa về công thức cấp số cộng lớp 11
Các ví dụ minh họa sẽ nâng cao kiến thức và khả năng áp dụng công thức cấp số cộng lớp 11 trong thế giới thực. Đây là một số ví dụ thông thường mà học sinh lớp mười một có thể tham khảo.
Một ví dụ: Tính số hạng của dãy cấp số cộng
- Giả sử một dãy cấp số cộng có số hạng đầu tiên là 5 và số công sai là 3. Hãy tính số dãy thứ mười.
- Giải thích: [a_n = a + (n-1)d] là công thức chung.
- Hãy sử dụng các giá trị đã biết trước đó: [a_10} = 5 + (10-1) ⋅ 3 = 5 + 27 = 32]
- Vì vậy, số hạng thứ mười hai là 32.
Ví dụ 2: Tính tổng của n số hạng của cấp số cộng
- Giả sử một dãy cấp số cộng có số hạng đầu tiên là 2, số công sai là 4 và bạn muốn tính tổng số hạng đầu tiên là 15.
- Giải thích: Đầu tiên, chúng ta phải tính số hạng cuối cùng, là số hạng thứ 15: [a_{15} = 2 + (15-1) cdot 4 = 2 + 56 = 58]
- Sau đó, hãy sử dụng công thức tính tổng sau: [S_n = n^2 + (a + l) = 15^2 + (2 + 58) = 15^2 + 60 = 15^2 + 30 = 450]
- Do đó, tổng số của 15 hạng đầu là 450.
Ví dụ 3: Ví dụ về việc sử dụng cấp số cộng trong thực tế
- Việc tiết kiệm tiền là một ví dụ thực tế về cấp số cộng. Giả sử bạn bắt đầu tiết kiệm 100.000 đồng và tăng thêm 50.000 đồng mỗi tháng. Hãy tính tổng số tiền bạn sẽ nhận được sau mười hai tháng.
- Giải: Số hạng đầu tiên là 100.000 đô la và công sai là 50.000 đô la. Tất cả những gì chúng tôi có là 650.000, vì a_{12} = 100.000 + (12-1) x 50.000 = 100.000 + 550.000 = 650.000.
- Sau mười hai tháng, tổng số tiền đã được thu được là 4.500.000 vì S=12 = frac12(2){6} (100.000 + 650.000) = 6 ]
- Sau mười hai tháng, bạn có tổng cộng 4.500.000 đồng.
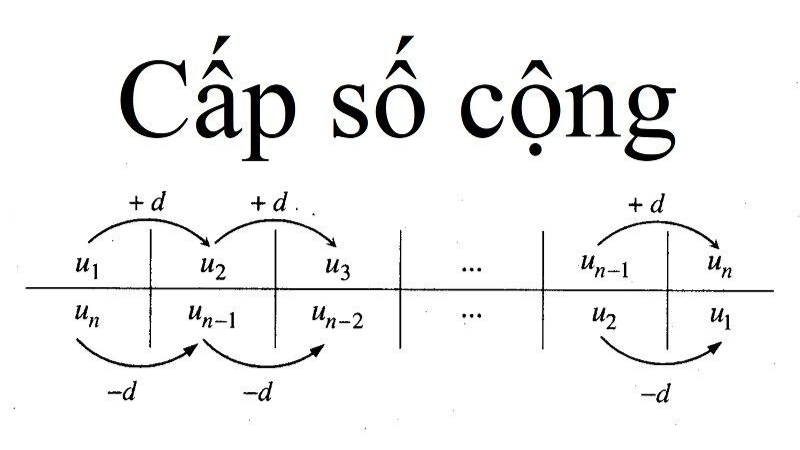
4. Ứng dụng thực tiễn của công thức cấp số cộng lớp 11
Cấp số cộng là một khái niệm lý thuyết với nhiều ứng dụng trong cuộc sống hàng ngày. Những ứng dụng này làm tăng nhận thức của học sinh về tầm quan trọng của cấp số cộng trong cuộc sống hàng ngày.
Tài chính
- Tài chính thường sử dụng cấp số cộng để tính toán tiền tiết kiệm hoặc đầu tư. Cấp số cộng sẽ giúp một người dự đoán số tiền họ sẽ nhận được sau một khoảng thời gian nhất định khi họ thực hiện các khoản đầu tư định kỳ với mức tăng đều.
- Chẳng hạn, nếu một người đầu tư một số tiền nhất định mỗi tháng và tăng thêm một khoản tiền đều đặn, việc tính toán tổng số tiền sẽ dễ dàng hơn với công thức cấp số cộng.
Trong các ngành khoa học và kỹ thuật
- Trong khoa học và kỹ thuật, nhiều hiện tượng tự nhiên và quy trình sản xuất được mô tả bằng cấp số cộng. Ví dụ, nghiên cứu vật lý sử dụng cấp số cộng để mô tả các chuyển động đồng đều. Điều này giúp các nhà khoa học phân tích và dự đoán hành vi của đối tượng.
- Ngoài ra, tính toán chính xác là cần thiết cho nhiều quy trình sản xuất trong ngành để tối ưu hóa chi phí và thời gian. Các nhà quản lý sản xuất nhận được lợi ích từ việc sử dụng cấp số cộng để tăng hiệu suất làm việc và cung cấp một cái nhìn tổng quan về quy trình.
Trong học thuật
- Cấp số cộng được sử dụng trong giáo dục trong nhiều lĩnh vực, không chỉ trong toán. Học sinh có thể giải quyết bài tập trong các lĩnh vực khoa học tự nhiên khác bằng cách sử dụng kiến thức về cấp số cộng. Điều này tạo nền tảng vững chắc cho việc học sau này.
- Hiểu biết về cấp số cộng cũng giúp học sinh phát triển các kỹ năng phân tích và tư duy logic, giúp họ trở thành những người giải quyết vấn đề hiệu quả hơn trong tương lai.
5. Lỗi thường gặp khi giải bài tập cấp số cộng
Học sinh thường mắc một số lỗi phổ biến khi làm bài tập liên quan đến công thức cấp số cộng lớp 11. Việc nhận diện và khắc phục những sai sót này sẽ giúp học tập hiệu quả hơn.
- Nhầm lẫn giữa số hạng đầu tiên và công sai: Nhầm lẫn giữa công sai và số hạng đầu tiên là một trong những lỗi phổ biến nhất. Sự khác biệt giữa các số hạng là công sai, trong khi số hạng đầu tiên là điểm bắt đầu của dãy. Kết quả sẽ không chính xác nếu một trong hai yếu tố này bị xác định sai.
- Tính toán sai khi thực hiện: Ngoài ra, lỗi tính toán là một vấn đề phổ biến. Do thiếu chú ý, học sinh đôi khi bỏ qua các bước tính toán hoặc tính toán sai trong bài tập. Một số bài tập sẽ cải thiện khả năng tính toán và sự chính xác.
- Không thử lại kết quả: Sau khi hoàn thành bài tập, nhiều học sinh không kiểm tra lại kết quả của mình. Vì vậy, có khả năng chấp nhận kết quả sai. Luôn luôn dành thời gian để kiểm tra lại các bước và kết quả cuối cùng của bài toán, điều này sẽ giúp đảm bảo rằng tính chính xác của bài toán là chính xác.

6. Kết luận
Chương trình toán học lớp 11 phải bao gồm công thức cấp số cộng lớp 11. Việc nắm vững kiến thức về cấp số cộng không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn trang bị cho họ những kiến thức cần thiết để ứng dụng trong cuộc sống thực tế. Chúc bạn thành công trong việc học tập và sẵn sàng cho kỳ thi! Ngoài ra bệnh giang mai cũng rất nguy hiểm bạn nên để ý.Trên đây là bài viết về công thức cấp số cộng lớp 11, chi tiết xin truy cập website: congthuccapsocong.com xin cảm ơn!
