Toán học là một lĩnh vực kỳ lạ trong đó những khái niệm đơn giản có thể dẫn đến một loạt các vấn đề phức tạp hơn. Cấp số cộng và cấp số nhân là hai khái niệm cơ bản mà bất kỳ người học toán nào cũng không thể bỏ qua. Chúng ta sẽ xem xét công thức cấp số cộng và cấp số nhân cũng như định nghĩa, đặc điểm, ứng dụng thực tiễn và các bài tập liên quan. Hy vọng rằng bạn sẽ có thể hiểu được hai khái niệm này trong vòng hai mươi phút.
1. Công thức cấp số cộng là gì?
Cấp số cộng (CSC) là một dãy số trong đó mỗi số hạng được tạo thành bằng cách cộng thêm một số cố định (được gọi là “công sai”) vào số hạng trước đó. Điều này tạo ra một chuỗi số tăng hoặc giảm đều đặn. Cấp số cộng không chỉ được tìm thấy trong toán học lý thuyết mà còn được tìm thấy trong các lĩnh vực như tài chính và khoa học.
Khái niệm về cấp số cộng rất quan trọng vì nó làm nền tảng cho nhiều lý thuyết toán học khác. Chúng ta sẽ xem xét định nghĩa cụ thể của cấp số cộng cũng như cách nó được sử dụng để tính toán. Điều này sẽ giúp chúng ta hiểu rõ hơn về cấp số cộng.
Ý nghĩa của cấp số cộng
Các yếu tố đầu tiên, công sai và số hạng thứ n tạo nên cấp số cộng. Dưới đây là các thành phần:
- Số hạng đầu tiên của dãy số được gọi là số hạng đầu tiên (a1).
- Công sai (d) là giá trị cố định được cộng vào tất cả các số hạng để tạo ra số hạng tiếp theo.
- Số hạng thứ n trong dãy số được gọi là số hạng thứ n (an).
- Sau đây là công thức tổng quát của cấp số cộng: [a_n = a_1 + (n – 1) \cdot d]
- Có thể dễ dàng tính số hạng trong dãy bằng cách sử dụng công thức này.
Một ví dụ cho thấy
Để làm rõ hơn khái niệm này, hãy cùng nhau xem xét một ví dụ đơn giản. Giả sử chúng ta có một dãy số bắt đầu từ hai và công sai của nó là ba. Sau đây là dãy số:
- Thứ nhất: Hai
- Hạng số thứ hai là 5: 2 + 3 = 5.
- Trong số hạng thứ ba, 5 plus 3 = 8.
- Trong số hạng thứ tư, 8 plus 3 = 11.
- Do đó, dãy số 2, 5, 8, 11,… sẽ tiếp tục. Đây là một ví dụ về cấp số cộng.
Vận dụng cấp số cộng
- Cấp số cộng có nhiều ứng dụng thực tiễn và lý thuyết. Các lĩnh vực như tài chính, vật lý hoặc kinh tế thường sử dụng nó.
- Tài chính: Trong việc tính toán lãi suất, nếu bạn gửi một khoản tiền nhất định vào ngân hàng với lãi suất cố định, số tiền gốc của bạn và lãi suất hàng tháng sẽ tạo thành một cấp số cộng.
- Kinh tế: Khi các nhà phân tích đưa ra giả định về tăng trưởng doanh thu hoặc chi phí, họ thường sử dụng cấp số cộng để dự báo tài chính trong một số năm tới.
Chúng ta nhận thấy rằng cấp số cộng là một khái niệm không thể thiếu trong nhiều lĩnh vực nghiên cứu và ứng dụng nhờ những ví dụ thực tế này.
2. Công thức tính cấp số nhân
Cấp số nhân (CSN) là một dãy số được tạo thành bằng cách nhân một số cố định (được gọi là “công bội”) với số hạng trước đó. Trong cấp số nhân, mối quan hệ giữa các hạng là mối quan hệ tỷ lệ, nghĩa là sự thay đổi ở mỗi hạng phụ thuộc vào cả số hạng trước và công bội. Điều này khác với cấp số cộng.
Chúng ta hãy xem xét các thành phần chính của nó để hiểu rõ hơn về cấu trúc và cách tính toán trong cấp số nhân.
Ý nghĩa của cấp số nhân
- Một dãy cấp số nhân được xác định bởi các thành phần sau:
- Số hạng đầu tiên (a1): Đây là số hạng đầu tiên của dãy số, giống như cấp số cộng.
- Công bội (q) là giá trị cố định mà chúng ta nhân với mỗi số hạng để tạo ra số hạng tiếp theo.
- Số hạng thứ n trong dãy số được gọi là số hạng thứ n (an).
- Có thể mô tả công thức tổng quát của cấp số nhân như sau: [a_n = a_1 \cdot q^{(n – 1)}]
- Công thức này cho phép nhanh chóng xác định số hạng trong dãy cấp số nhân.
Một ví dụ cho thấy
- Chúng ta hãy xem xét một ví dụ cụ thể để minh họa điều này. Giả sử dãy số bắt đầu từ ba và công bội là hai. Sau đây là dãy số được tạo thành:
- Hạng đầu tiên là 3, hạng thứ hai là 3 x 2 = 6.
- Trong số thứ ba, 6 x 2 = 12.
- Trong số thứ tư, 12 x 2 = 24.
- Dãy số có dạng 3, 6, 12, 24 và như vậy. Ví dụ này cho thấy sự phát triển nhanh chóng của cấp số nhân.
Vận dụng cấp số nhân
- Cấp số nhân cũng rất quan trọng trong đời sống hàng ngày và trong các lĩnh vực chuyên ngành.
- Khoa học tự nhiên: Cấp số nhân có thể được sử dụng để mô tả nhiều hiện tượng sinh học, chẳng hạn như sự phát triển của cây cối hoặc sinh sản của vi khuẩn.
- Tài chính: Khi lãi suất được tính trên cả số vốn ban đầu và lãi suất trong các kỳ trước, cấp số nhân cũng được sử dụng.
Nhìn chung, cấp số nhân là lý thuyết và có thể được sử dụng để phân tích và dự đoán nhiều sự kiện thực tế.
2. So sánh công thức cấp số cộng và cấp số nhân
Mặc dù có nhiều điểm tương đồng giữa các khái niệm về công thức cấp số cộng và cấp số nhân, nhưng hai khái niệm này cũng rất khác nhau. Nắm bắt những so sánh này giúp chúng ta áp dụng công thức đúng đắn trong các bài toán.
Cách tạo dãy số
- Một cấp số cộng được tạo ra bằng cách cộng một số cố định vào tất cả các hạng trước đó. Mặt khác, cấp số nhân hình thành được tạo ra bằng cách nhân một số cố định vào từng hạng trước đó.
- Điều này dẫn đến sự khác biệt trong sự biến đổi giữa hai loại dãy số. Trong khi cấp số nhân tăng nhanh hoặc giảm dần tùy thuộc vào công sai, cấp số cộng tạo ra sự tăng trưởng đều đặn.
Tính chất và lợi ích
- Tính lãi suất đơn hoặc dự báo doanh thu yêu cầu cấp số cộng. Mặt khác, các lĩnh vực như sinh học, vật lý và tài chính thường sử dụng cấp số nhân để tính lãi suất kép.
- Sự khác biệt này cho thấy tác động của mỗi loại cấp số và cách chúng được sử dụng trong thực tế.
Đồ thị hiển thị
- Bạn sẽ thấy một đường thẳng với độ dốc ổn định khi vẽ đồ thị của cấp số cộng, trong khi đồ thị của cấp số nhân sẽ có hình dạng cong với độ dốc tăng dần hoặc giảm dần nhanh chóng. Điều này cho thấy sự khác biệt rõ ràng trong tốc độ biến đổi giữa hai loại dãy số.
Nhìn chung, việc so sánh cấp số cộng và cấp số nhân không chỉ giúp bạn hiểu rõ hơn về chúng mà còn giúp bạn giải quyết các bài toán cụ thể một cách hiệu quả.

3. Ứng dụng của công thức cấp số cộng và cấp số nhân
Cả cấp số cộng và cấp số nhân đều quan trọng trong nhiều lĩnh vực. Trong các lĩnh vực từ kinh tế đến tài chính và khoa học tự nhiên, những ứng dụng này không chỉ giúp giải quyết vấn đề mà còn nâng cao hiệu quả nghiên cứu và công việc.
Các lĩnh vực tài chính và kinh tế
- Tài chính sử dụng cấp số cộng để tính lãi suất đơn, trong khi cấp số nhân thường được sử dụng để tính lãi suất kép. Lãi suất kép tính lãi trên cả vốn và lãi đã sinh ra, nhưng lãi suất đơn chỉ tính trên số vốn ban đầu.
- Trong lĩnh vực tài chính, hai loại cấp số này không chỉ giúp các nhà đầu tư đưa ra quyết định tốt hơn mà còn tạo ra cơ hội sinh lời lớn hơn cho các cá nhân và công ty.
Công nghệ tự nhiên
- Khoa học tự nhiên thường sử dụng cấp số nhân để mô tả các vấn đề như phát triển dân số, sự lây lan của bệnh dịch hoặc phản ứng hóa học. Những mô hình này cho phép các nhà nghiên cứu dự đoán và giải quyết các vấn đề ngay lập tức.
- Cấp số cộng cũng có thể được sử dụng để mô tả những hiện tượng như sự phát triển của thực vật theo thời gian hoặc chu trình nước, đặc biệt là trong nông nghiệp.
Đào tạo
- Việc dạy cấp số cộng và cấp số nhân trong lớp học giúp học sinh phát triển tư duy logic và khả năng phân tích. Thường xuyên trong chương trình học, các bài toán liên quan đến hai loại cấp số này được sử dụng để giúp học sinh làm quen với các khái niệm cơ bản của toán học.
4. Các dạng bài tập công thức cấp số cộng và cấp số nhân
Bài tập liên quan đến cả cấp số cộng và cấp số nhân rất phong phú và đa dạng. Chúng có thể bao gồm các câu hỏi liên quan đến tính số hạng và áp dụng trong các tình huống cụ thể.
Bài tập liên quan đến việc cộng số
- Trong các bài tập cấp số cộng, học sinh thường phải tính toán số hạng của dãy số, tính tổng hoặc xác định công sai. Bạn có thể phải đối mặt với một bài tập như: “Cho dãy số 3, 7, 11, 15.” Hãy tính tổng của mười số cao nhất.”
- Bài tập này cải thiện khả năng tính toán của bạn và giúp bạn hiểu cách các cấp số cộng hoạt động.
Bài tập liên quan đến số nhân
- Các bài tập liên quan đến số nhân cũng rất đa dạng. Những bài tập này thường yêu cầu học sinh tính số hạng, tính tổng hoặc áp dụng công thức vào các tình huống thực tế. Một ví dụ thông thường là: “Cho dãy số 2, 6, 18, 54. Hãy tính số thứ sáu trong dãy số này.
- Bạn sẽ cải thiện khả năng tính toán của mình bằng cách sử dụng công thức cấp số nhân trong bài tập này.
Bài tập kết hợp
- Ngoài các bài tập về cấp số cộng và cấp số nhân riêng lẻ, đôi khi bạn cũng sẽ được yêu cầu hoàn thành các bài tập tổng hợp yêu cầu bạn kết hợp cả hai loại cấp số này. Đây là một bài kiểm tra thú vị sẽ nâng cao kiến thức của bạn và khả năng tư duy của bạn.
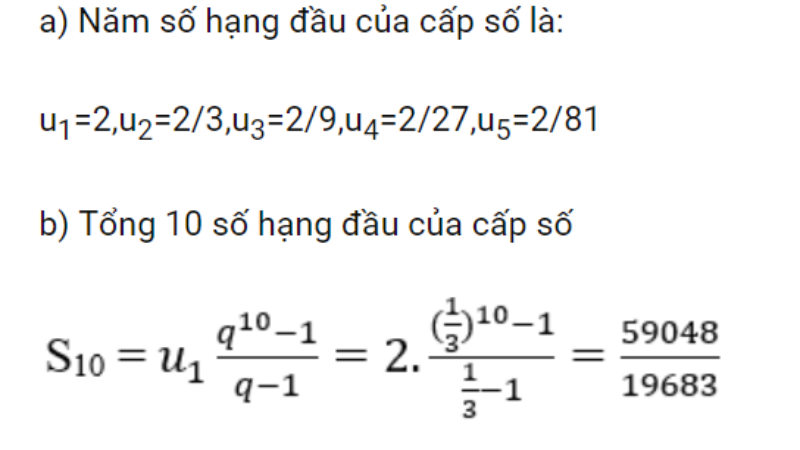
5. Lời giải chi tiết cho bài toán công thức cấp số cộng và cấp số nhân
Việc hiểu rõ công thức cấp số cộng và cấp số nhân và phương pháp là rất quan trọng khi giải quyết các bài toán liên quan đến cấp số cộng và cấp số nhân. Đây là một số cách giải quyết hiệu quả.
Giải quyết bài toán về cấp số cộng
- Xác định số hạng đầu tiên và công sai là bước đầu tiên khi giải bài toán cấp số cộng. Sau đó, để xác định số hạng bất kỳ, bạn có thể sử dụng công thức [a_n = a_1 + (n – 1) \cdot d]. Bạn có thể sử dụng công thức tổng của cấp số cộng trong trường hợp bài toán yêu cầu tính tổng của các số hạng: [S_n = frac{n}{2} cdot (a_1 + a_n) ]
- Giải quyết bài toán một cách nhanh chóng và chính xác sẽ dễ dàng hơn nếu bạn áp dụng các công thức đúng cách.
Giải quyết bài toán có cấp số nhân.
- Bạn cũng cần xác định số hạng đầu tiên và công bội trong các bài toán cấp số nhân. Tìm số hạng thứ n bằng cách sử dụng công thức: [a_n = a_1 \cdot q^{(n – 1)} ]. Công thức tổng của cấp số nhân phải được sử dụng nếu bài toán yêu cầu tính tổng: [S_n = a_1 ⋅ frac{1 – q^n}{1 – q}] (với (q không bằng 1)).
Ví dụ trong thực tế
- Giải quyết một bài toán cho cả cấp số cộng và cấp số nhân với nhau sẽ là một ví dụ.
- Cấp số cộng: Giả sử có một dãy số từ 5 đến 15…. với tỷ lệ công sai là 5 Tính tổng của hai mươi số đầu tiên. Số hạng đầu tiên (a1) = 5, công sai (d) = 5, và số hạng thứ hai (a20) = 5 + (20 – 1) 5 = 100. Tổng số hạng đầu tiên của 20 số (S20) = 20/2 (5 + 100) = 1050.
- Cấp số nhân: Giả sử một dãy số có các số 3, 9, 27,… với công bội là 3. Tính số hạng thứ năm cũng như tổng số hạng thứ năm. Số hạng đầu tiên (a1) là 3, số hạng công bội (q) là 3, số hạng thứ năm (a5) là 3 và số hạng thứ ba (a3) là 3 3(5-1) = 243. Tổng của năm số hạng đầu tiên (S5) = 3 (1 – 3 5)/(1 – 3) = 363.
6. Các cách học nhanh công thức cấp số cộng và cấp số nhân
Để học các công thức cấp số cộng và cấp số nhân, cần phải sử dụng các phương pháp học tập hiệu quả. Một số phương pháp sẽ giúp bạn học nhanh và nhớ lâu.
Sử dụng các biểu đồ tư duy
- Sơ đồ tư duy là một công cụ hữu ích để ghi nhớ và tổ chức thông tin. Bạn sẽ dễ dàng hình dung và kết nối các yếu tố bằng cách vẽ sơ đồ cho các khái niệm cấp số cộng và cấp số nhân.
- Các thành phần như số hạng đầu tiên, công sai, công bội, công thức tính, ứng dụng và ví dụ minh họa có thể là một phần của sơ đồ tư duy. Điều này sẽ hỗ trợ não bộ ghi nhớ trực quan.
Thực hành hàng ngày
- Bất kỳ môn học nào cũng cần thực hành, và toán học cũng không phải là ngoại lệ. Bạn nên làm các bài tập về cấp số cộng và cấp số nhân, từ dễ đến khó.
- Hãy thử các bài tập tính số hạng và tính tổng. Bạn sẽ trở nên thành thạo hơn trong việc áp dụng công thức khi làm quen với các bài toán.
Hợp tác với nhóm học tập
- Một cách tuyệt vời để trao đổi kiến thức và giải quyết các vấn đề khó khăn là học nhóm. Khi bạn làm việc trong một nhóm, bạn có thể thảo luận về các khái niệm về cấp số cộng và cấp số nhân, chia sẻ các phương pháp giải quyết bài toán và hỗ trợ lẫn nhau.
- Điều này không chỉ cải thiện kiến thức mà còn tạo ra một môi trường học tập sáng tạo và tích cực.
7. Lợi ích khi biết công thức cấp số cộng và cấp số nhân
Nắm vững các công thức cấp số cộng và cấp số nhân không chỉ giúp bạn dễ dàng hoàn thành bài tập toán học mà còn có nhiều lợi ích khác trong cuộc sống hàng ngày.
Ứng dụng trong thế giới thực
- Biết các công thức cấp số cộng và cấp số nhân cho phép bạn áp dụng kiến thức này vào các tình huống thực tế. Tính toán lãi suất ngân hàng, dự đoán xu hướng tiêu dùng hoặc thậm chí là lập kế hoạch tài chính cá nhân là mọi thứ bạn có thể làm nhanh chóng.
- Hiểu cách các dãy số này phát triển sẽ giúp bạn đưa ra những quyết định tốt hơn.
Tăng cường tư duy logic
- Học số cộng và nhân không chỉ dạy bạn các công thức mà còn dạy bạn suy nghĩ logic và phân tích.
- Bạn sẽ trở nên linh hoạt hơn trong cách suy nghĩ và xử lý thông tin khi học cách giải quyết vấn đề.
Cơ hội công việc
- Tóm lại, biết cách sử dụng cấp số cộng và cấp số nhân có thể giúp bạn tiếp cận nhiều cơ hội nghề nghiệp. Tài chính, kinh tế, khoa học dữ liệu và phân tích thống kê là những nghề nghiệp yêu cầu nền tảng toán học vững chắc.
8. Kết luận
Trong toán học, công thức cấp số cộng và cấp số nhân là hai khái niệm cơ bản nhưng quan trọng. Bạn không chỉ có thể giải quyết các bài toán dễ dàng hơn mà còn có nhiều cơ hội hơn trong cuộc sống nếu bạn hiểu chúng. Bạn hãy xem review đồ ăn để kiếm những món ăn ngon bồi bổ sau những giờ học tập mệ mỏi.
Mục đích của bài viết này là giúp bạn hiểu rõ hơn về các công thức cấp số cộng và cấp số nhân, từ định nghĩa, đặc điểm, ứng dụng và cách học hiệu quả. Để thành công trong học tập và trong cuộc sống, hãy luôn cố gắng áp dụng những kiến thức này! Trên đây là bài viết về công thức cấp số cộng và cấp số nhân, chi tiết xin truy cập website: congthuccapsocong.com xin cảm ơn!
