Công thức của cấp số cộng là một khái niệm quan trọng trong toán học và không có nhiều ứng dụng trong cuộc sống hàng ngày. Chúng tôi sẽ xem xét kỹ thuật lưỡng thức cấp số cộng , bao gồm các định nghĩa, các thành phần của nó, cách tính toán và các ứng dụng của nó trong toán học
1. Công thức của cấp số cộng là gì?
Công thức của cấp số cộng được tạo ra bằng cách cộng một số cố định (được gọi là sai ) thành số đứng trước khi nó được gọi là cộng số cấp. Vì vậy, dãy số 2, 5, 8, 11, 14 là một số cộng cấp với sai công bằng 3 . Sau đây là chung công thức của cộng cấp :
- a, a + d, a + 2d, a + 3d,… a + (n-1)d
Nó bao gồm:
- Số đầu tiên của số là a .
- Sai số d là cộng vào tất cả các số để được số tiếp theo .
- Các số trong số được gọi là n .
- Do đó, chỉ cần biết số đầu (a), sai công (d) và vị trí của số trong số cấp (n), công thức của cộng số cấp cho phép chúng tôi xác định bất kỳ số nào trong số cấp đó .

2. Ứng dụng của công thức cấp số cộng trong toán học
Trong học toán , công thức cấp số cộng có nhiều công dụng quan trọng, đặc biệt là :
Tính tổng các số trong cấp số cộng:
- Công thức của cấp số cộng công thức tính tổng các số là S = n/2 * (a + l), trong đó l là số cuối cùng của cấp số.
- Chẳng hạn, hãy tính tổng các số từ 3 đến 15 (cấp số cộng với a=3, d=2 và n=7). Khi sử dụng công thức, chúng tôi tìm thấy S = 7/2 * (3 + 15) = 63.
Giải bài toán liên quan đến cấp số cộng:
- Công thức của cấp số cộng Khi bạn biết một số khác trong cấp số cộng, hãy tìm số đầu, công sai hoặc số lượng.
- Tìm công sai của cấp số cộng 2, 5, 8, 11, 14 trong ví dụ này.
Mô tả các mô hình hàm số:
- Các mô hình hàm số tuyến tính có thể được mô tả bằng cấp số cộng.
- Quan hệ giữa số lượng sản phẩm và thời gian trong quá trình sản xuất là một ví dụ.
- Do đó, công thức của cấp số cộng đóng một vai trò quan trọng trong việc mô tả các mô hình toán học và giải quyết một số bài toán thực tế.
Các yếu tố của công thức cấp số cộng
- Công thức của cấp số cộng Trăm yếu tố chính được bao gồm trong công thức của cấp số cộng:
- Số đầu (a): Số đứng đầu của cấp số cộng. Nó quyết định giá trị cấp số bắt đầu.
- Công sai (d) là số cố định được cộng vào tất cả các số để tạo ra số tiếp theo. Khoảng cách giữa các số trong cấp số được xác định bởi công sai.
- Số lượng số (n): tổng số số trong cấp số cộng. Nó xác định thời gian của cấp số.
- Vì ba yếu tố này quyết định hình dạng và chức năng của cấp số cộng, nên mối quan hệ giữa chúng rất quan trọng. Ta có thể dễ dàng tính toán yếu tố còn lại nếu biết hai trong ba yếu tố này.
Cách tính tổng trong cấp số cộng
Công thức của cấp số cộng là một trong những sử dụng quan trọng nhất của công thức cấp số cộng. Sau đây là công thức tính tổng:
- S = n/2 * (a + l)
- Nó bao gồm:
- S là tổng các số trong cấp số cộng n và cấp số a là số đầu tiên.
- Cấp số cuối cùng có số l.
- Tính tổng các số từ 5 đến 17 trong cấp số cộng, ví dụ.
- Số đầu (a) là năm.
- Công sai (d) lớn hơn 3.
- Số số (n) bằng 17 – 5/3 trừ 1 là 5
- Khi sử dụng công thức, chúng ta có: S = 5/2 *(5 +17) = 55
- Do đó, tổng cộng có 55 số từ 5 đến 17.
3. Sự khác biệt giữa cấp số cộng và cấp số nhân
Có hai loại cấp số: cấp số cộng và cấp số nhân. Một số cố định có thể được cộng và nhân để tạo ra cấp số cộng và cấp số nhân.
- Nói cách khác, các cấp số cộng như a, a+d, a+2d, a+3d và a+(n-1)d.
- Ngoài ra, có các cấp số nhân như a, ar và ar^2., ar3,…(+1)
- Sự khác biệt quan trọng nhất giữa hai loại cấp số này là:
- Phép cộng và nhân được sử dụng cho cấp số cộng và nhân.
- Công sai (d) là số cố định được cộng trong cấp số cộng và tỷ số (r) là số cố định được nhân trong cấp số nhân.
- Trong khi cấp số nhân có sự khác biệt bằng nhau giữa các số liên tiếp, thì cấp số cộng có sự khác biệt bằng nhau giữa các số liên tiếp.
- Khi giải các bài toán liên quan, cần phải phân biệt rõ ràng hai loại cấp số này.
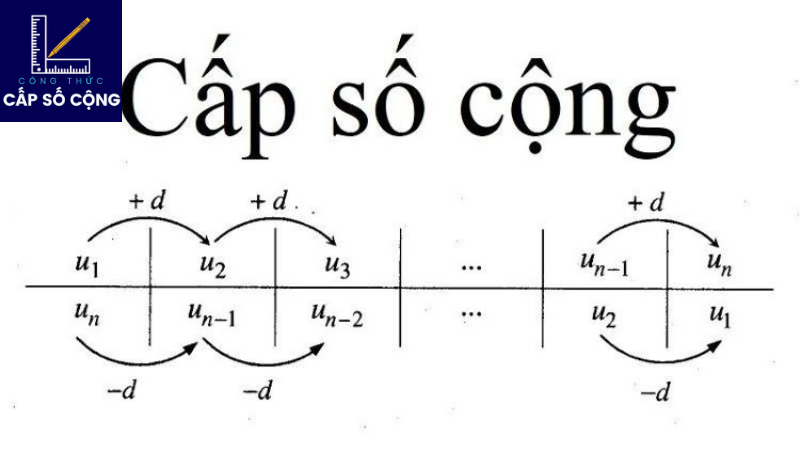
4. Giải bài tập liên quan đến công thức cấp số cộng
Chúng ta hãy giải một số bài tập thông thường công thức của cấp số cộng để ôn tập và làm quen với công thức cấp số cộng:
Bài 1: Cho cấp số cộng 3, 7, 11, 15, …, 35. Hãy tìm công sai và số lượng các số trong cấp số.
Giải:
- Số đầu (a) = 3
- Số cuối (l) = 35
- Để tìm công sai (d), ta dùng công thức: l = a + (n-1)d
- Thay số liệu vào, ta có: 35 = 3 + (n-1)d
- Giải phương trình này, ta tìm được d = 4 và n = 8.
Vậy công sai của cấp số cộng là 4, và số lượng các số trong cấp số là 8.
Bài 2: Tính tổng các số trong cấp số cộng 4, 7, 10, 13, …, 22.
Giải:
- Số đầu (a) = 4
- Công sai (d) = 3
- Số lượng số (n) = (22 – 4)/3 + 1 = 7
Áp dụng công thức tính tổng: S = n/2 (a + l) S = 7/2 (4 + 22) S = 91
Vậy tổng các số trong cấp số cộng là 91.
Các ví dụ trên cho thấy rằng việc hiểu công thức cấp số cộng và các kỹ năng sử dụng chúng là rất quan trọng để giải quyết các bài toán liên quan.

5. Kết luận
Công thức của cấp số cộng là một công cụ toán mạnh mạnh được sử dụng rộng rãi trong nhiều lĩnh vực , bao gồm giải bài toán , tính tổng và mô hình hoá mối mối quan hệ tuyến tính. Chúng tôi đã xem xét định nghĩa, các thành phần của nó, cách tính toán và những điều khác biệt giữa cấp số cộng và cấp số nhân. Hi vọng rằng bạn đã nắm vững cách áp dụng công thức cấp số cộng đồng để giải quyết các bài toán thực tế nhờ các ví dụ minh họa .
Như vậy, với công thức tính tổng và số hạng tổng quát của cấp số cộng, chúng ta có thể dễ dàng giải quyết các bài toán liên quan đến dãy số có quy luật cộng dồn không đổi. Hiểu rõ những công thức này sẽ giúp việc tính toán trở nên nhanh chóng và hiệu quả hơn. Bệnh zona, chi tiết xin truy cập website congthuccapsocong.com xin cảm ơn!

